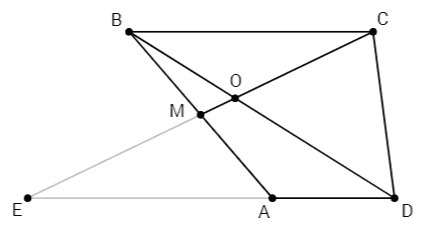
В трапеции ABCD точка M лежит на середине боковой стороны AB, диагональ BD пересекает отрезок CM в точке O. Найти площадь треугольника COD, если площадь треугольника BOM равна 1 и CO=4 OM
Ответы
Площади треугольников с равными высотами относятся как длины сторон, на которые опущены эти высоты. (теорема).
В ∆ ВОМ и ∆ ВОС высота ВЕ общая, СО=4МО, следовательно,
S ∆ ВОС= 4S∆BOM=4.
Из вершины А проведем параллельно СМ прямую до пересечения с BD в точке Т.
АМ=ВМ по условию, АТ║МО по построению ⇒ для ∆ АВТ отрезок МО - средняя линия. ⇒ BO=TO
∆ ВМО~∆ ABT, k= BM/BA=1/2.
Рассмотрим ∆ DAT и ΔBOC.
∠ADT=∠OBC - внутренние накрестлежащие при пересечении оснований трапеции диагональю BD,
∠ATD=∠BOC - внешние накрестлежащие при пересечении АТ║СМ секущей BD. ⇒
∆ DAT~∆ BOC по 1-му признаку подобия.
AT:OM=2(найдено); CO:OM=4 (дано) ⇒ CO:AT=4:2=2
Отсюда следует отношение ВО:DT=2 ⇒ DT=0,5BO;
DO=1,5BO.
Высота СН общая для ∆BOC и ∆COD, следовательно,
S ∆COD=1,5S∆ BOC=4•1,5=6
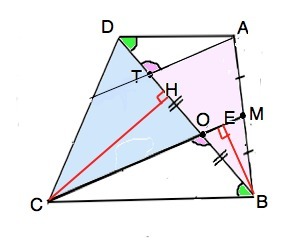
CM=CO+OM=5OM
△EMA=△BMC (MA=BM, ∠MAE=∠MBC накрест лежащие при AD||BC, ∠EMA=∠BMC вертикальные)
EM=CM => EO=EM+OM=CM+OM=6OM
EO/CO=6OM/4OM=3/2
△EOD~△BOC (∠ODE=∠OBC, ∠OED=∠OCB накрест лежащие при AD||BC)
OD/BO=EO/CO=3/2
S△= 1/2 *ab *sin(a):
S△COD/S△BOM= CO*OD/OM*BO = 4*3/2 =6 <=> S△COD =6