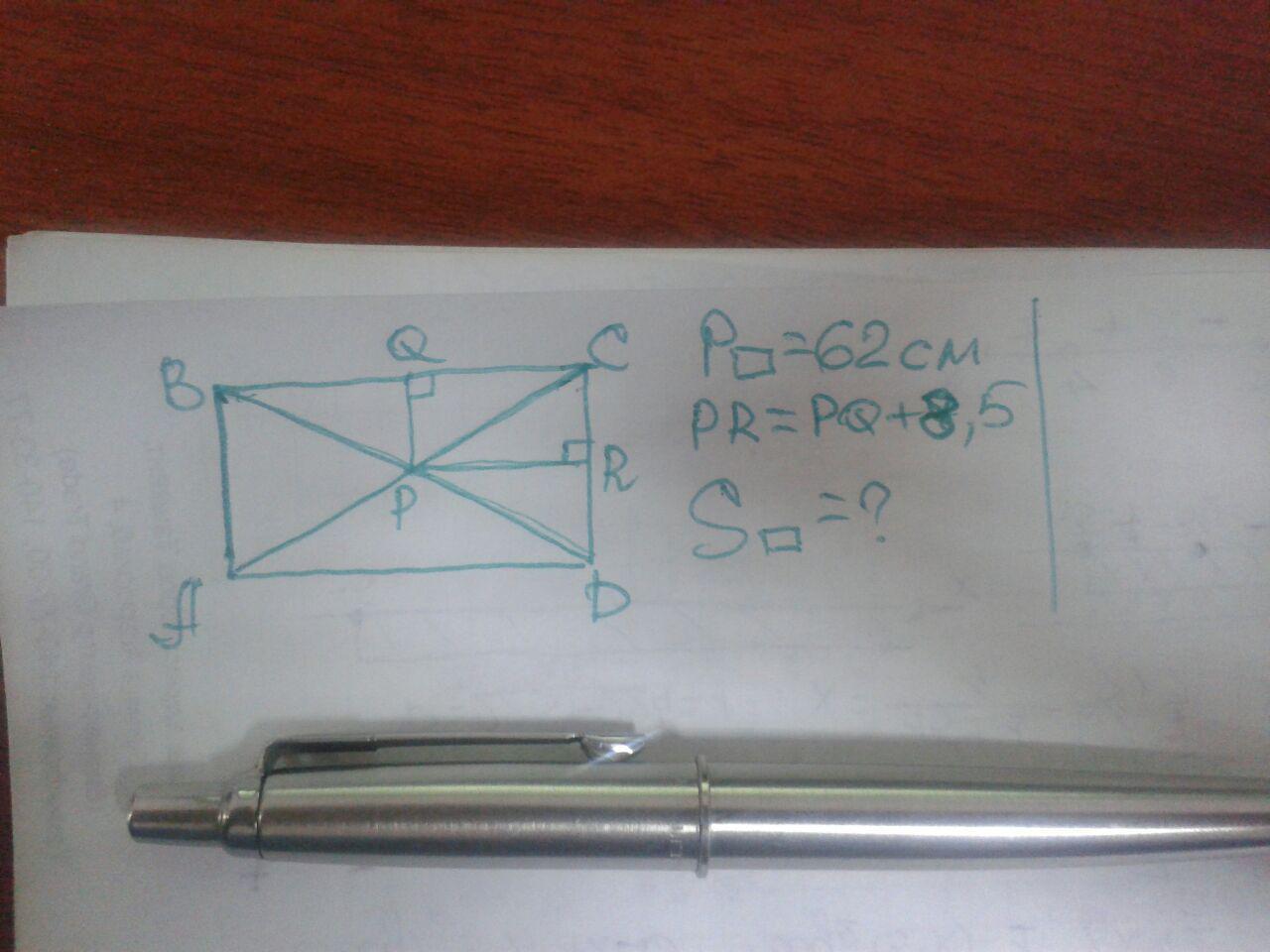
найти площадь прямоугольника периметра которого равен 62 см если точка пересечения его диагоналей отстоит от меньшей стороны на 8,5 см дальше чем от большей стороны

Рассмотрите такое решение:
1. Как показано на наброске, отрезок PQ||AB и 2PQ=AB. То же относится и к паре PR-BC.
2. Поэтому ВС-АВ=17 см. (так как PQ&PR - половины сторон прямоугольника). Следовательно, зная периметр, можно найти стороны прямоугольника: 2АВ+2ВС=62 ⇒ АВ+ВС=31 ⇒ 2АВ+17=31, откуда АВ=7. Значит, ВС=24.
3. Площадь прямоугольника равна: АВ*ВС=24*7=168.
Просьба по возможности перепроверить расчёты.