Предмет: Алгебра, автор: MERRY191

помогитеее)решить пожалуйста

Приложения:

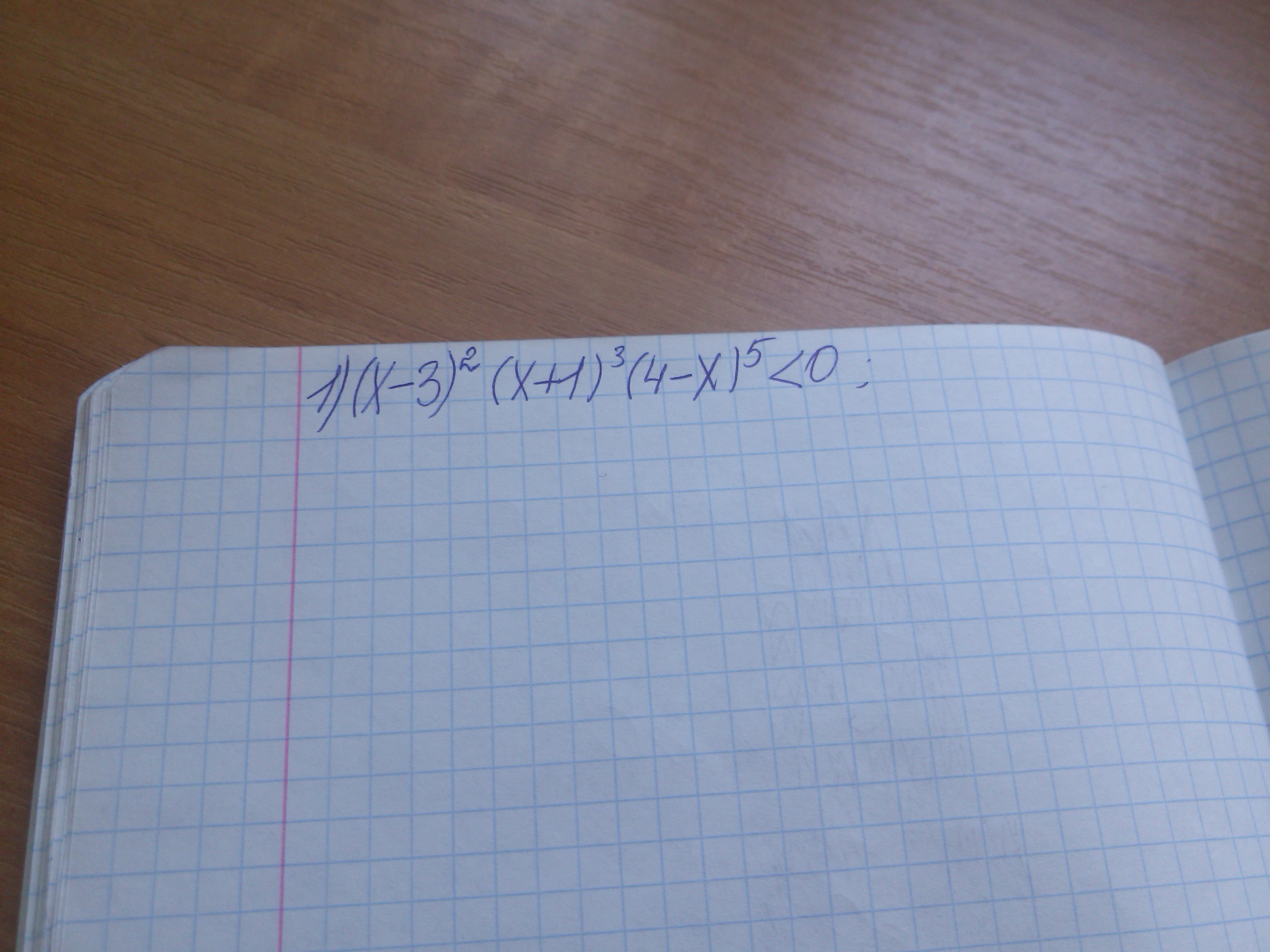
Ответы

Автор ответа: Kornella

Это задание решается методом интервалов:
1) заменим неравенство уравнением: (x-3)^2(x+1)^3(4-x)^5=0
Произведение равно нули когда хотя бы один из множителей равен нулю, поэтому :
x=3( заметьте знак степени четный, следовательно знаки на координатной прямой будут одинаковые)
x=-1(степень нечетная-знаки меняются)
x=4(степень также нечетная и знаки меняются)
2) отмечаем эти корни на координатной прямой
- + + -
-1 3 4

3) Смотрим на знак неравенства <, следовательно выбираем промежутки со знаком минус, то есть: xE(-∞;-1)U(4;+∞)
Ответ:xE(-∞;-1)U(4;+ ∞)

Автор ответа: AnonimusPro

двучлен (x-3)^2 - в квадрате, значит он всегда больше 0 и его можно не учитывать при решении неравенства, но так как неравенство строгое, то его корень не будет входить в промежуток решений неравенства.
$(x-3)^2 \neq 0 \\x \neq 3$
остальные находятся в нечетной степени, следовательно при определении знаков можно их степени мысленно откинуть.
находим корни оставшихся двучленов:
$(x+1)^3=0 \\x=-1 \\(4-x)^5=0 \\x=4$
теперь определяем знаки:
на (-oo;-1)
берем -2
(-1)*6 - знак (-)
на (-1;3)
берем 0
1*4 - знак (+)
на (3;4)
берем 3,5
4,5*(0,5) - знак (+)
на (4;+oo)
берем 5
4*(-1) - знак (-)
значит промежуток решения данного неравенства $x \in (-\infty;-1) \cup(4;+\infty)$
Ответ: $x \in (-\infty;-1) \cup(4;+\infty)$

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Литература, автор: 13Ilya14

Что способствовало росту популярности песни «Русское поле»? Расскажите об истории создания песни и поразмышляйте о том, что помогает современной песне стать широко известной и даже «уйти в народ», как это было с лучшими авторскими песнями в 19 веке. Могут ли в наши дни авторы песен стать такими же «безвестными», как народные поэты Суриков, Кольцов или Никитин? ПОМОГИТЕ ПОЖАЛУЙСТА,КРАТКО,ДАЮ 100 БАЛОВ

1 год назад

Предмет: Математика, автор: ilonanazaryk0

Допоможіть із математикою будь-ласка
1)-78+(-16);
2)-34+(-66);
3)-102+(-28);
4)-97+(-33);
5)-87(-17);
6)-85+(-55);
7)-63+(-77);
8)-10,2+(-0,11);
9)-4,5+(-0,6);
10)-2,2+(-5,8);
11)-3,46+(-6,98);
12)-20(-3,26);
13)-9,1+(-0,09);
14)-0,2+(-0,8)

1 год назад

Предмет: Алгебра, автор: kostpetrenko8

помогите пожалуста !

1 год назад

Предмет: Математика, автор: NikolaevaDasha555

Для линейного уравнения 6x+4y -12=0 найдите значение y, если x=0

7 лет назад

Предмет: Французский язык, автор: ZnanijaLiza

Помогите пожалуйста

7 лет назад