Предмет: Геометрия,
автор: Dимасuk
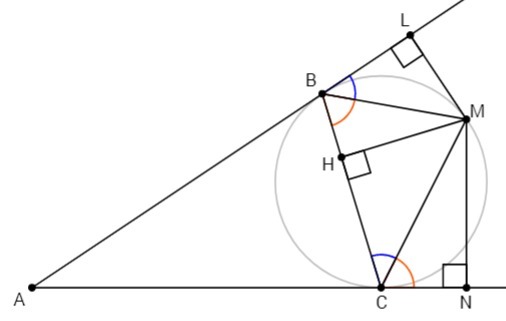
В острый угол BAC вписана окружность (B и C - точки касания). На большей дуге BC отмечена точка M. К прямым AB и AC опущены перпендикуляры ML и MN. На прямую BC опущен перпендикуляр MH.
Докажите, что LM·MN= MH².
Задача с похожим условием уже была на сайте, но, к сожалению, не решена.
Скорее всего, тут нужно рассмотреть подобие ΔMLH и ΔLNH.
Ответы
Автор ответа:
0
∠MBL= ∪BM/2 (Угол между касательной и хордой, проведенной в точку касания, равен половине дуги, стягиваемой хордой.)
∠MCB= ∪BM/2 (Вписанный угол равен половине дуги, на которую опирается.)
∠MBL=∠MCB
Аналогично ∠MBC=∠MCN
△MBL ~ △MCH => ML/MH = MB/MC
△MBH ~ △MCN => MH/MN = MB/MC
ML/MH = MH/MN <=> MH^2= ML*MN
∠MCB= ∪BM/2 (Вписанный угол равен половине дуги, на которую опирается.)
∠MBL=∠MCB
Аналогично ∠MBC=∠MCN
△MBL ~ △MCH => ML/MH = MB/MC
△MBH ~ △MCN => MH/MN = MB/MC
ML/MH = MH/MN <=> MH^2= ML*MN
Приложения:
Интересные вопросы
Предмет: Физика,
автор: stasgorovenko64
Предмет: Русский язык,
автор: Ruslanafresh
Предмет: Русский язык,
автор: Аноним
Предмет: Математика,
автор: олеся562
Предмет: Химия,
автор: SHKOLNIK013