Предмет: Физика, автор: RusSskiI

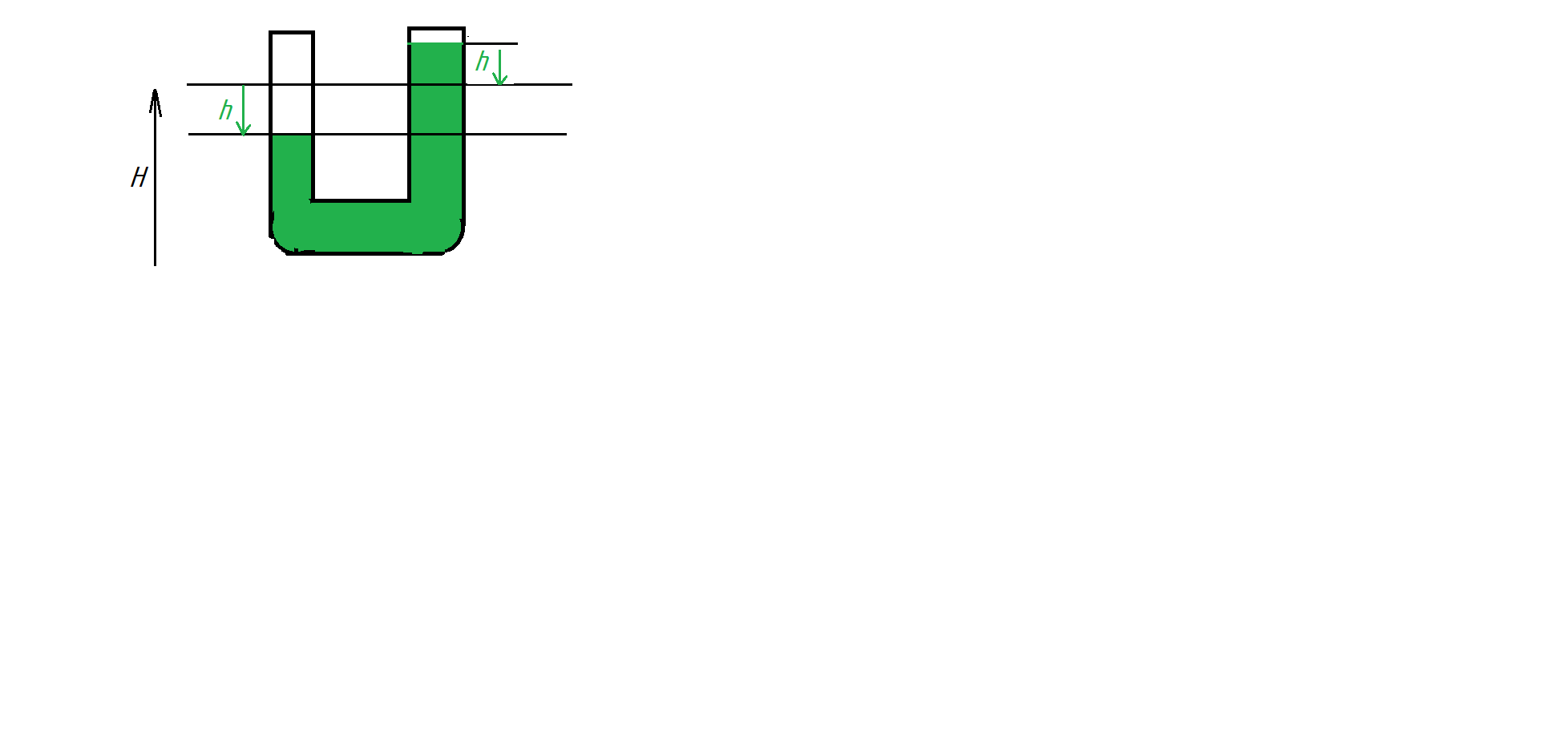
Ртуть массой m колеблется в дугообразном (U) сосуде, площадь поперечного сечения которого S. Найти период.

Ответы

Автор ответа: PhysM

1 способ:
При выводе жидкости из равновесия, возникает возвращающая сила:
$F=2rho gSDelta h$
Которая действует на всю жидкость.
Находим ускорение из второго закона Ньютона:
$a=cfrac{F}{m}=cfrac{2rho gSDelta h}{m}$
Массу найдем как сумму масс в обеих частях:
$m=m_1+m_2=2rho SH$
Получаем:
$a=cfrac{gh}{H}$
Так как движение колебательное, присутствует циклическая частота:
$a=w^2h=cfrac{gh}{H}\w^2=cfrac{g}{H}\w=sqrt{cfrac{g}{H}}$
Тогда период будет равен:
$T=cfrac{2pi}{w}=2pisqrt{cfrac{H}{g}}$
2 способ:
Колебания жидкости в сосуде можно сопоставить с колебаниями математического маятника:
$w=sqrt{cfrac{g}{H}}=sqrt{cfrac{k}{m}}\w=sqrt{cfrac{k}{2rho SH}}\k=2rho gS$
Аналогично находится период, подстановкой циклической частоты.
$T=sqrt{cfrac{m}{k}}$

Приложения:

Автор ответа: PhysM

в нашем случаем вместо S берем высоту h

Автор ответа: PhysM

разобрались?

Автор ответа: RusSskiI

Да, вроде бы. Спасибо ещё раз.

Автор ответа: PhysM

Рад что помог

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Биология, автор: plmnkoijyttg

До коротких кісток скелета належать пліз скоро я на уроці

6 лет назад

Предмет: Английский язык, автор: liza8239

D Correct the words in bold.
1 This DVD is me.
2 They house is beautiful.
3 This isn't my pencil. It's she
4 No, it isn't Bob and Martha's. It's us!
5 I parents live here
6 He loves he car.

6 лет назад

Предмет: Українська мова, автор: Аноним

ПОМОГИТЕ!
Лише особові форми дієслова записані в рядку

А початися, готувати, плести
Б розбиває, несеш, розквітає
В посіявши, осиротілий, жартуючи
Г може, зробити, знаючи

6 лет назад

Предмет: Химия, автор: Dasha8274

Назовите следующие вещества: а) CH3-CH2-CH(CH3)-CH3 б) CH3-CH(CH3)-CH2-CH-(CH3)-CH3 d) CH2=CH-CH(C2H5)-CH3 e) CH5C=C-H3 d) CH3-CH2-C-(CH3)=C-(CH3)-CH3 f) C6H6

10 лет назад

Предмет: Обществознание, автор: Elizzavetta

В следующих утверждениях что-то перепутано:

1.Превосходство в должности,социальном положении, закрепленное конституцией, уставом ,законом, традицией,-пример влияния через силу

2.Превосходство в физических качествах или вооружении-пример влияния через свой авторитет.

3.Превосходство в обаянии, компетентности,знаниях,нравственных качествах, популярности - пример влияния с помощью власти

10 лет назад