Предмет: Алгебра,
автор: maxxx2000
Решите вот это уравнение
Приложения:
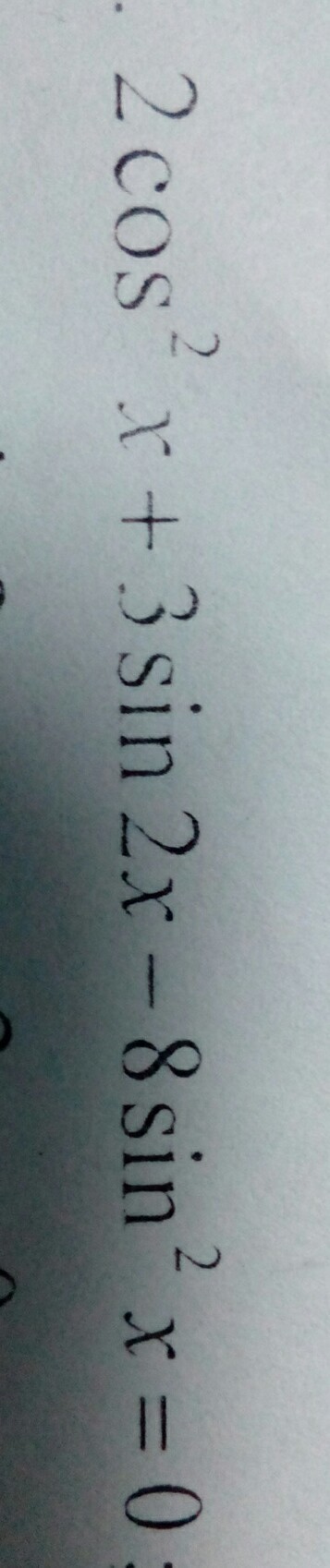
Ответы
Автор ответа:
0
делаем замену:
обратная замена:
ответ:
Автор ответа:
0
у котангенса наименьший положительный период равен pi, а не 2pi
Автор ответа:
0
2сos²x + 3sin2x - 8sin²x = 0
Разложим синус удвоенного аргумента:
2cos²x + 6sinxcosx - 8sin²x = 0
cos²x + 3sinxcosx - 4sin²x = 0 |:sin²x
ctg²x + 3ctgx - 4 = 0
Пусть t = ctgx.
t² + 3t - 4 = 0
t₁ + t₂ = -3
t₁t₂ = -4
t₁ = -4
t₂ = 1
Обратная замена:
ctgx = 1
x = π/4 + πn, n ∈ Z
ctgx = -4
x = arcctg(-4) + πn, n ∈ Z
Ответ: x = π/4 + πn, n ∈ Z; arcctg(-4) + πn, n ∈ Z.
Разложим синус удвоенного аргумента:
2cos²x + 6sinxcosx - 8sin²x = 0
cos²x + 3sinxcosx - 4sin²x = 0 |:sin²x
ctg²x + 3ctgx - 4 = 0
Пусть t = ctgx.
t² + 3t - 4 = 0
t₁ + t₂ = -3
t₁t₂ = -4
t₁ = -4
t₂ = 1
Обратная замена:
ctgx = 1
x = π/4 + πn, n ∈ Z
ctgx = -4
x = arcctg(-4) + πn, n ∈ Z
Ответ: x = π/4 + πn, n ∈ Z; arcctg(-4) + πn, n ∈ Z.
Интересные вопросы
Предмет: История,
автор: novickovav56
Предмет: Українська мова,
автор: vikadovhaliuk
Предмет: Биология,
автор: dt9565185
Предмет: Математика,
автор: 100004
Предмет: Математика,
автор: angel77783