Предмет: Алгебра, автор: Vili1111

Решите алгебру!
постройте график функции:
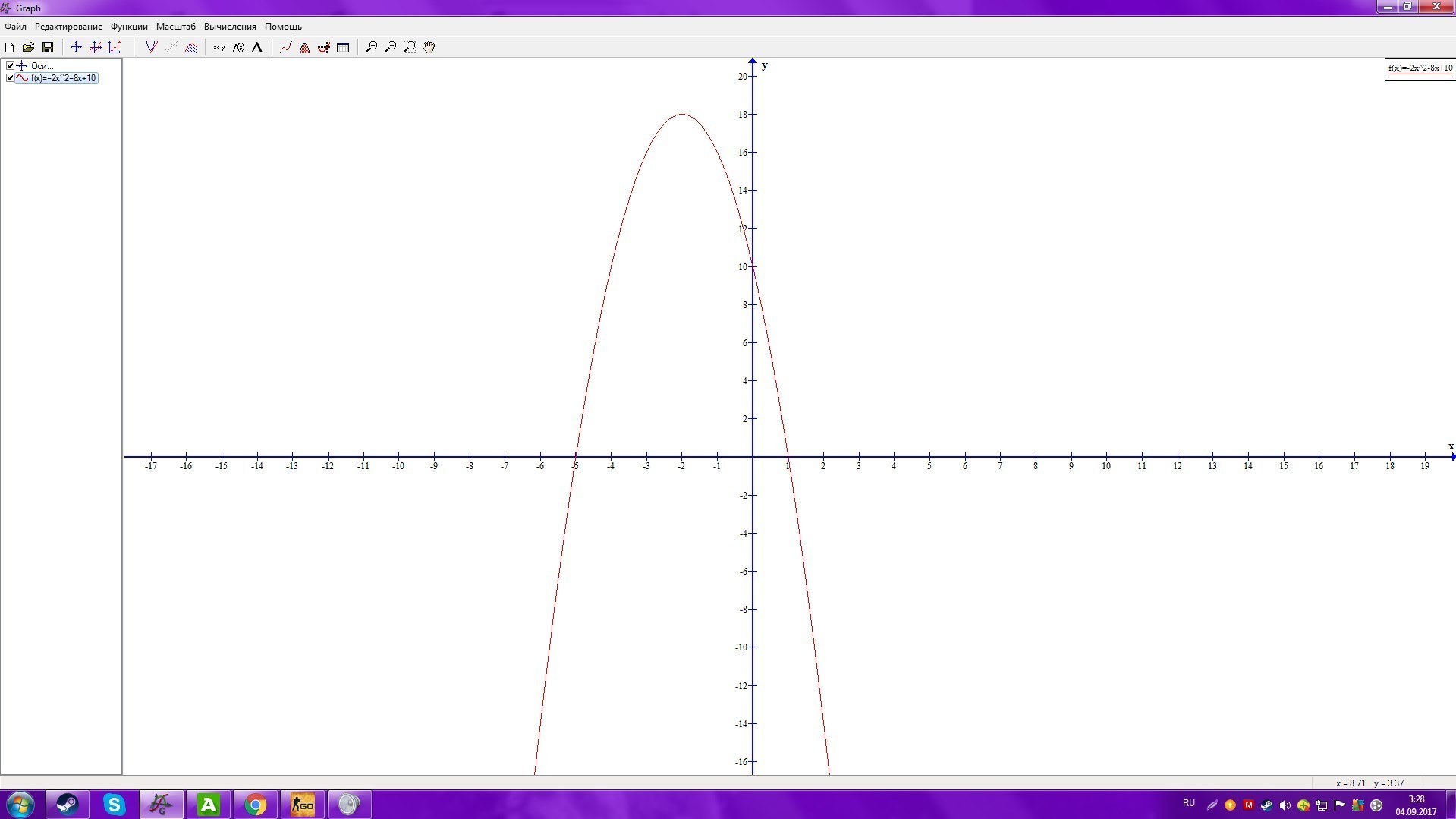
y= -2x^ -8x + 10
укажите промежуток :
-функция возрастает
-функция положителена

Ответы

Автор ответа: skvrttt

итак, $mathtt{f(x)=-2x^2-8x+10=-2(x^2+4x-5)=-2(x+5)(x-1)}$ ; (график во вложении, если не понял)

второе задание:
чтобы узнать, на каком промежутке функция возрастает/убывает, для начала нам необходимо найти производную данной функции:

$mathtt{f'(x)=(-2x^2-8x+10)'=(-2x^2)'-(8x)'=-4x-8=-4(x+2)}$

во-вторых, нам необходимо приравнять производную к нулю, чтобы найти критические точки, расставить интервалы и выяснить, на каких интервалах производная функции отрицательна и, наконец, на каких – положительна:

$mathtt{-4(x+2)=0}$ , следовательно, производная имеет единственную критическую точку $mathtt{x=-2}$ ; интервалы нам дают следующее: производная отрицательна на промежутке $mathtt{xin(-2;+infty)}$ , следовательно, функция на этом промежутке убивает, и наоборот, – возрастает функция на промежутке $mathtt{xin(-infty;-2)}$ , потому что производная на данном промежутке положительна.

ответ: $mathtt{xin(-infty;-2)}$

третье задание:
чтобы узнать, при каких икс функция принимает тот или иной знак, нам понадобится вспомнить приём неравенств; наша заданная функция $mathtt{f(x)=-2(x+5)(x-1)}$ должна быть положительна, следовательно, неравенство мы получаем следующее: $mathtt{-2(x+5)(x-1) textgreater 0}$ ; решение неравенства: $mathtt{(x+5)(x-1) textless 0~to~xin(-5;1)}$

ответ: $mathtt{xin(-5;1)}$