Предмет: Геометрия,
автор: KnowledgePower
Решить данную задачу.
Приложения:
Ответы
Автор ответа:
0
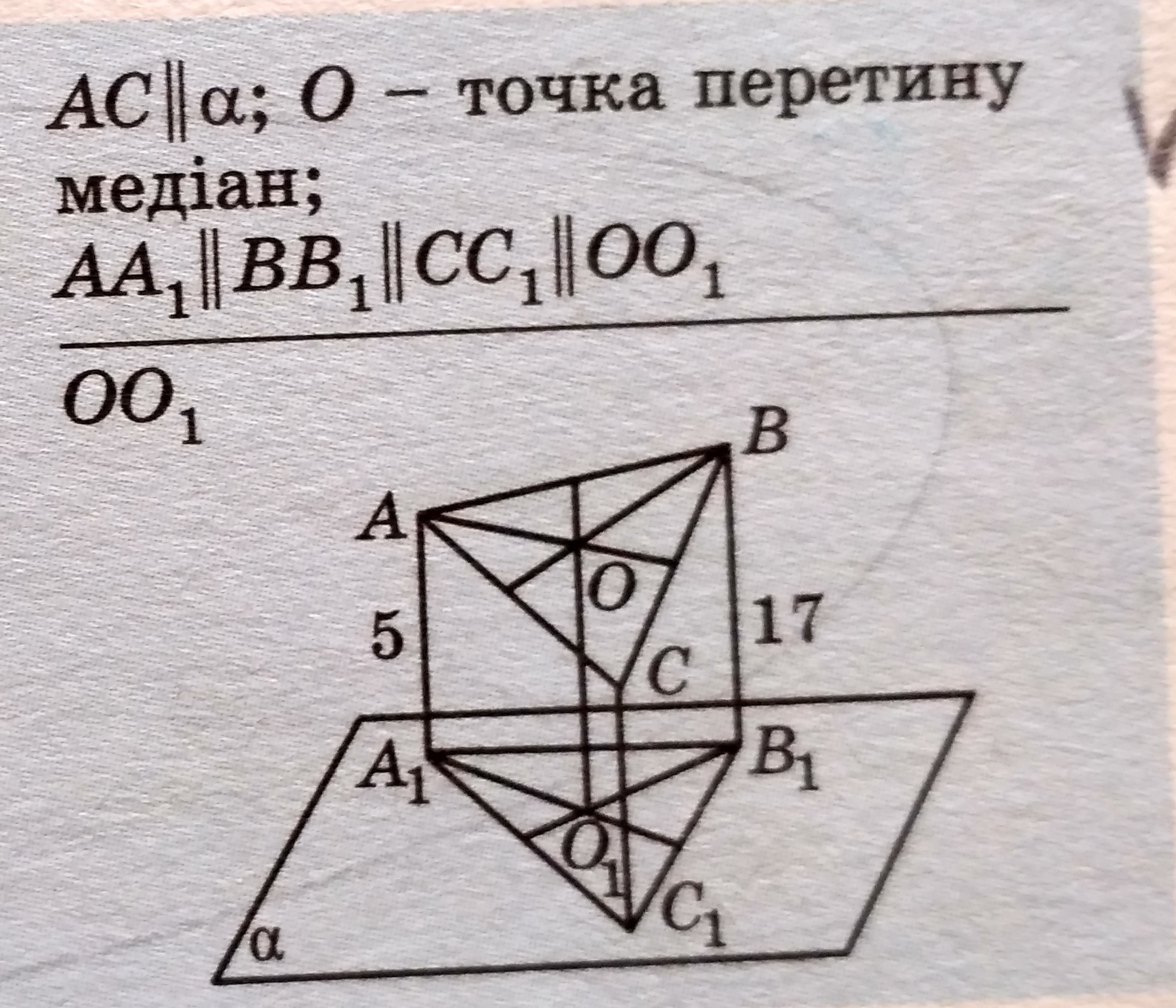
Так как АА₁ || СС₁ и АС || α (а значит и АС || А₁С₁), то А₁АСС₁ - параллелограмм. СС₁=АА₁=5 как противоположные стороны параллелограмма.
Проведем плоскость β || α через сторону АС. Пусть эта плоскость пересекает отрезок ВВ₁ в точке Н, а отрезок ОО₁ в точке М.
BB₁=BH+B₁H
OO₁=OM+O₁M
Так как отрезки АА₁, ВВ₁, СС₁, ОО₁ параллельны, то АА₁=СС₁=В₁H=О₁М=5.
Тогда:
OO₁=OM+O₁M
ВВ₁=ВH+В₁H; ВH=ВВ₁-В₁H=17-5=12
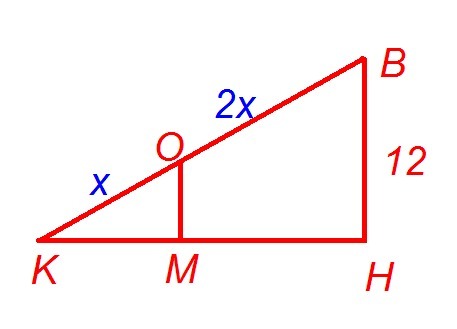
Проведем проекцию НК медианы BК. Рассмотрим подобные по двум углам треугольники OMK и BHK. Составим отношение сходственных сторон, учитывая, что медианы точкой пересечения делятся в отношении 2:1, считая от вершины:
![frac{OM}{OK} = frac{BH}{BK}
\
ON = frac{BH}{BK} cdot OK
\
OM = frac{12}{2x+x} cdot x=4](https://tex.z-dn.net/?f=+frac%7BOM%7D%7BOK%7D+%3D+frac%7BBH%7D%7BBK%7D+%0A%5C%0AON+%3D+frac%7BBH%7D%7BBK%7D+cdot+OK%0A%5C%0AOM+%3D+frac%7B12%7D%7B2x%2Bx%7D+cdot+x%3D4 "frac{OM}{OK} = frac{BH}{BK}
\
ON = frac{BH}{BK} cdot OK
\
OM = frac{12}{2x+x} cdot x=4")
OO₁=OM+O₁M=4+5=9
Ответ: 9
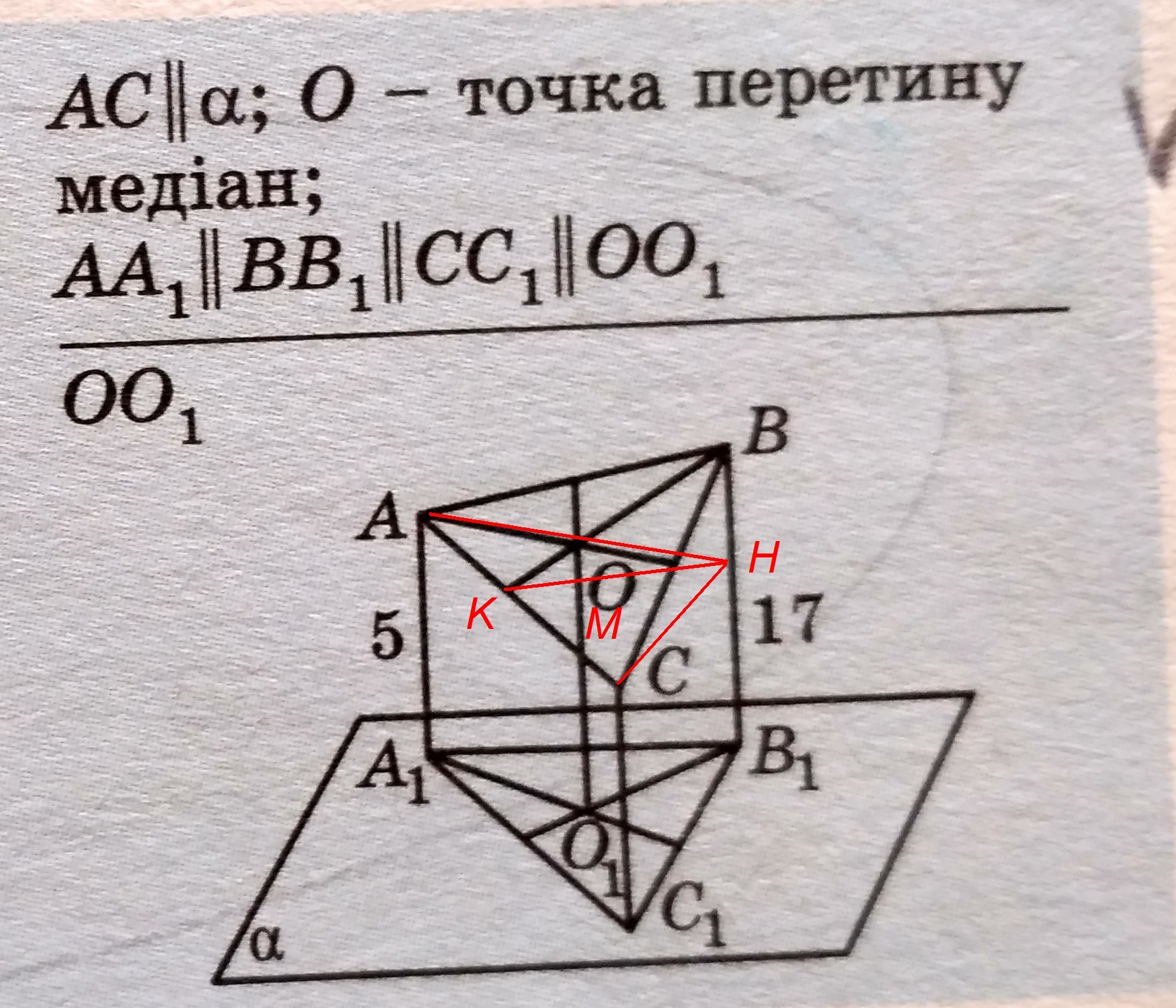
Проведем плоскость β || α через сторону АС. Пусть эта плоскость пересекает отрезок ВВ₁ в точке Н, а отрезок ОО₁ в точке М.
BB₁=BH+B₁H
OO₁=OM+O₁M
Так как отрезки АА₁, ВВ₁, СС₁, ОО₁ параллельны, то АА₁=СС₁=В₁H=О₁М=5.
Тогда:
OO₁=OM+O₁M
ВВ₁=ВH+В₁H; ВH=ВВ₁-В₁H=17-5=12
Проведем проекцию НК медианы BК. Рассмотрим подобные по двум углам треугольники OMK и BHK. Составим отношение сходственных сторон, учитывая, что медианы точкой пересечения делятся в отношении 2:1, считая от вершины:
OO₁=OM+O₁M=4+5=9
Ответ: 9
Приложения:
Интересные вопросы
Предмет: Физика,
автор: unicornmasha62
Предмет: Алгебра,
автор: TemchikGo
Предмет: Обществознание,
автор: beastteam2202
Предмет: Экономика,
автор: lenavavilova
Предмет: География,
автор: w12345678908