Начертите параллелограм ABCD и постройте векторы 2/3CB+CD, и 1/4 (BA-BC)

Ответ:

Построение на рисунке.

Объяснение:

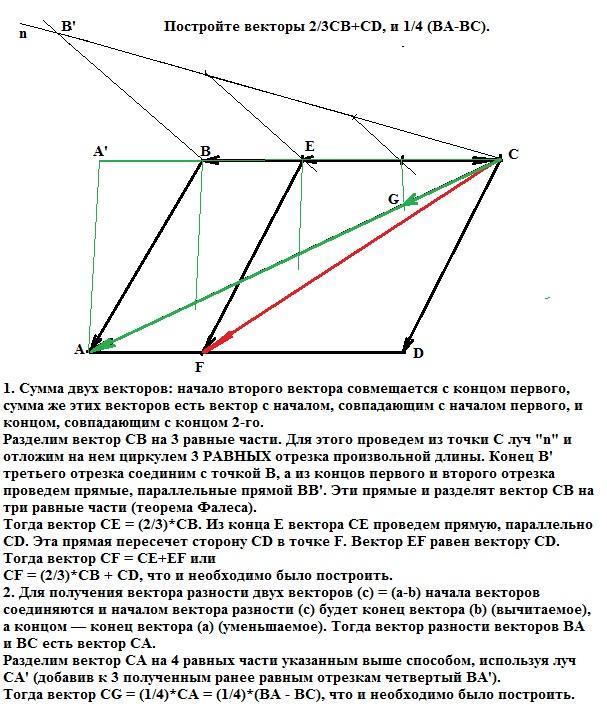
1. Сумма двух векторов: начало второго вектора совмещается с концом первого,  сумма же этих векторов есть вектор с началом, совпадающим с началом первого, и концом, совпадающим с концом 2-го.

Разделим вектор CB на 3 равные части. Для этого проведем из точки С луч "n" и отложим на нем циркулем 3 РАВНЫХ отрезка произвольной длины. Конец B' третьего отрезка соединим с точкой В, а из концов первого и второго отрезка проведем прямые, параллельные прямой BB'. Эти прямые и разделят вектор СВ на три равные части (теорема Фалеса).

Тогда вектор СЕ = (2/3)*СВ. Из конца Е вектора СЕ проведем прямую, параллельно CD. Эта прямая пересечет сторону CD в точке F. Вектор EF равен вектору CD. Тогда вектор CF = CE+EF или

CF = (2/3)*CB + CD, что и необходимо было построить.

2. Для получения вектора разности двух векторов (c) = (a-b) начала векторов соединяются и началом вектора разности (c) будет конец вектора (b) (вычитаемое), а концом - конец вектора (a) (уменьшаемое). Тогда вектор разности векторов ВА и ВС есть вектор СА.

Разделим вектор СА на 4 равных части указанным выше способом, используя луч СA' (добавив к 3 полученным ранее равным отрезкам четвертый BA').

Тогда вектор CG = (1/4)*СА = (1/4)*(ВА - ВС), что и необходимо было построить.