Привет! Помогите решить задачу по геометрии:
На медиане CM треугольника ABC обозначили точки K и E так, что угол AKM = 90 градусов, и CE = 2MK.
Нужно доказать что BE = AC

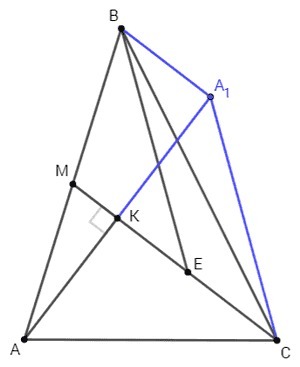
A1∈AK, AK=KA1

MK - средняя линия △ABA1 (AK=KA1, AM=MB) =>
BA1=2MK; BA1||MK (BA1||CE)

BA1=2MK=CE

BA1CE - параллелограмм (сторона BA1 равна и параллельна стороне CE) =>
BE=A1C

△ACA1 - равнобедренный (∠AKC=90, AK=KA1, CK является медианой и высотой) =>
AC=A1C

BE=A1C=AC