Предмет: Алгебра,
автор: ansys222
Необходимо разложить многочлен на множители
Приложения:
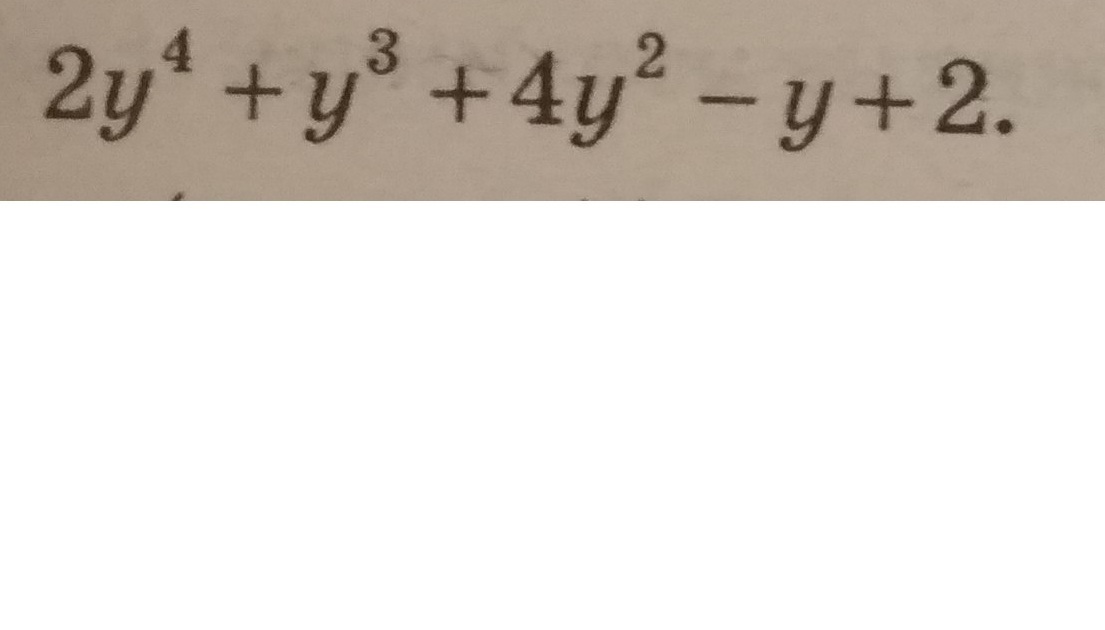
Ответы
Автор ответа:
0
Многочлен 4-ой степени первый коэффициент которого 2(!) и последний 2 (!) можно представить в виде многочленов второй степени так
2y⁴+y³+4y²-y+2=(y²+Ay+1)*(2y²+Cy+2) (1)
или
2y⁴+y³+4y²-y+2=(y²+Ay+2)*(2y²+Cy+1) (2)
Раскрываем скобки:
2y⁴+y³+4y²-y+2=2y⁴+(2A+C)y³+(4+AC)y²+(2A+C)y+2
Два многочлена равны, если у них одинаковые степени и коэффициенты при одинаковых степенях переменной совпадают.
2A+C=1
4+AC=4
2A+C=-1
Первая и третья строка противоречат друг другу, значит разложение (1) невозможно
2y⁴+y³+4y²-y+2=(y²+Ay+2)*(2y²+Cy+1) (2)
Раскрываем скобки:
2y⁴+y³+4y²-y+2=2y⁴+(2A+C)y³+(4+AC+1)y²+(2С+А)y+2
Два многочлена равны, если у них одинаковые степени и коэффициенты при одинаковых степенях переменной совпадают.
2A+C=1 ⇒ C=1-2A
4+AC+1=4
2С+A=-1 ⇒C= (-1-A)/2
1-2A=(-1-A)/2
2-4A=-1-A
3=3A
A=1
C=-1
О т в е т.
2y⁴+y³+4y²-y+2=(y²+y+2)*(2y²-y+1)
2y⁴+y³+4y²-y+2=(y²+Ay+1)*(2y²+Cy+2) (1)
или
2y⁴+y³+4y²-y+2=(y²+Ay+2)*(2y²+Cy+1) (2)
Раскрываем скобки:
2y⁴+y³+4y²-y+2=2y⁴+(2A+C)y³+(4+AC)y²+(2A+C)y+2
Два многочлена равны, если у них одинаковые степени и коэффициенты при одинаковых степенях переменной совпадают.
2A+C=1
4+AC=4
2A+C=-1
Первая и третья строка противоречат друг другу, значит разложение (1) невозможно
2y⁴+y³+4y²-y+2=(y²+Ay+2)*(2y²+Cy+1) (2)
Раскрываем скобки:
2y⁴+y³+4y²-y+2=2y⁴+(2A+C)y³+(4+AC+1)y²+(2С+А)y+2
Два многочлена равны, если у них одинаковые степени и коэффициенты при одинаковых степенях переменной совпадают.
2A+C=1 ⇒ C=1-2A
4+AC+1=4
2С+A=-1 ⇒C= (-1-A)/2
1-2A=(-1-A)/2
2-4A=-1-A
3=3A
A=1
C=-1
О т в е т.
2y⁴+y³+4y²-y+2=(y²+y+2)*(2y²-y+1)
Автор ответа:
0
решение конечно нетривиальное, а оно сойдет на уровень 10 класса ?
Автор ответа:
0
конечно, другого решения просто нет. Данный многочлен не имеет действительных корней, потому раскладывается на два квадратных трехчлена с отрицательными дискриминанатми
Интересные вопросы
Предмет: Английский язык,
автор: Masha7517
Предмет: Химия,
автор: pupgtopchuk
Предмет: Русский язык,
автор: sanchospanvhos2011
Предмет: Математика,
автор: лейла151
Предмет: Математика,
автор: olgademidenko8