Предмет: Алгебра,
автор: Fovden
Пожалуйста помогите найти производную.
Приложения:
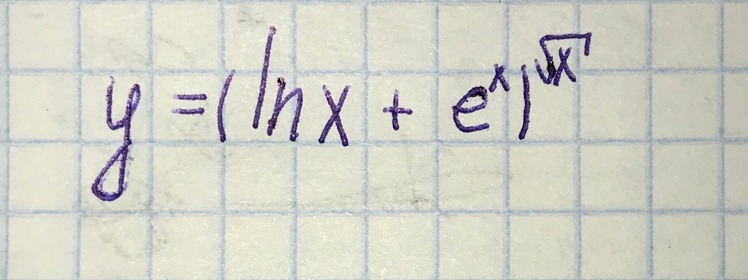
Ответы
Автор ответа:
0
производная сложно-показательной функции:
1)логарифмируем левую и правую часть функции:
2) упрощаем
3) берем производную от левой и правой частей функции
4) выражаем y'
![y=(lnx+e^x)^{ sqrt{x} } \ \ lny=ln[(lnx+e^x)^{ sqrt{x} }] \ \lny=sqrt{x} ln[(lnx+e^x) \ \ (lny)'=(sqrt{x} )' ln[(lnx+e^x)] +(ln[(lnx+e^x)])' sqrt{x} \ \ frac{1}{y} *y'= frac{1}{2sqrt{x}} ln[(lnx+e^x)]+ frac{1}{lnx+e^x} *( frac{1}{x}+e^x) sqrt{x} \ \ y'=y [frac{1}{2sqrt{x}} ln[(lnx+e^x)]+ frac{1}{lnx+e^x} *( frac{1}{x}+e^x) sqrt{x} ] \](https://tex.z-dn.net/?f=y%3D%28lnx%2Be%5Ex%29%5E%7B+sqrt%7Bx%7D+%7D+%5C+%5C+lny%3Dln%5B%28lnx%2Be%5Ex%29%5E%7B+sqrt%7Bx%7D+%7D%5D+%5C+%5Clny%3Dsqrt%7Bx%7D++ln%5B%28lnx%2Be%5Ex%29+%5C+%5C+%28lny%29%27%3D%28sqrt%7Bx%7D+%29%27++ln%5B%28lnx%2Be%5Ex%29%5D+%2B%28ln%5B%28lnx%2Be%5Ex%29%5D%29%27+sqrt%7Bx%7D++%5C++%5C++frac%7B1%7D%7By%7D+%2Ay%27%3D+frac%7B1%7D%7B2sqrt%7Bx%7D%7D+++ln%5B%28lnx%2Be%5Ex%29%5D%2B+frac%7B1%7D%7Blnx%2Be%5Ex%7D+%2A%28+frac%7B1%7D%7Bx%7D%2Be%5Ex%29++sqrt%7Bx%7D+%5C+%5C+y%27%3Dy++%5Bfrac%7B1%7D%7B2sqrt%7Bx%7D%7D+++ln%5B%28lnx%2Be%5Ex%29%5D%2B+frac%7B1%7D%7Blnx%2Be%5Ex%7D+%2A%28+frac%7B1%7D%7Bx%7D%2Be%5Ex%29++sqrt%7Bx%7D++%5D+%5C+ "y=(lnx+e^x)^{ sqrt{x} } \ \ lny=ln[(lnx+e^x)^{ sqrt{x} }] \ \lny=sqrt{x} ln[(lnx+e^x) \ \ (lny)'=(sqrt{x} )' ln[(lnx+e^x)] +(ln[(lnx+e^x)])' sqrt{x} \ \ frac{1}{y} *y'= frac{1}{2sqrt{x}} ln[(lnx+e^x)]+ frac{1}{lnx+e^x} *( frac{1}{x}+e^x) sqrt{x} \ \ y'=y [frac{1}{2sqrt{x}} ln[(lnx+e^x)]+ frac{1}{lnx+e^x} *( frac{1}{x}+e^x) sqrt{x} ] \")
Так как
то конечный ответ:
![y'=(lnx+e^x)^{ sqrt{x} } [frac{1}{2sqrt{x}} ln[(lnx+e^x)]+ frac{1}{lnx+e^x} *( frac{1}{x}+ e^x) sqrt{x} ] = \ \ = y'=(lnx+e^x)^{ sqrt{x} } [frac{ln[(lnx+e^x)]}{2sqrt{x}} + frac{1}{lnx+e^x} *( frac{ sqrt{x}}{x}+ e^x) ]](https://tex.z-dn.net/?f=y%27%3D%28lnx%2Be%5Ex%29%5E%7B+sqrt%7Bx%7D+%7D++%5Bfrac%7B1%7D%7B2sqrt%7Bx%7D%7D+++ln%5B%28lnx%2Be%5Ex%29%5D%2B+frac%7B1%7D%7Blnx%2Be%5Ex%7D+%2A%28+frac%7B1%7D%7Bx%7D%2B+e%5Ex%29++sqrt%7Bx%7D++%5D+%3D+%5C+%5C+%3D+y%27%3D%28lnx%2Be%5Ex%29%5E%7B+sqrt%7Bx%7D+%7D++%5Bfrac%7Bln%5B%28lnx%2Be%5Ex%29%5D%7D%7B2sqrt%7Bx%7D%7D+++%2B+frac%7B1%7D%7Blnx%2Be%5Ex%7D+%2A%28+frac%7B+sqrt%7Bx%7D%7D%7Bx%7D%2B+e%5Ex%29++%5D "y'=(lnx+e^x)^{ sqrt{x} } [frac{1}{2sqrt{x}} ln[(lnx+e^x)]+ frac{1}{lnx+e^x} *( frac{1}{x}+ e^x) sqrt{x} ] = \ \ = y'=(lnx+e^x)^{ sqrt{x} } [frac{ln[(lnx+e^x)]}{2sqrt{x}} + frac{1}{lnx+e^x} *( frac{ sqrt{x}}{x}+ e^x) ]")
![OTBET: y'=(lnx+e^x)^{ sqrt{x} } [frac{ln[(lnx+e^x)]}{2sqrt{x}} + frac{1}{lnx+e^x} *( frac{ sqrt{x}}{x}+ e^x) ]](https://tex.z-dn.net/?f=OTBET%3A++y%27%3D%28lnx%2Be%5Ex%29%5E%7B+sqrt%7Bx%7D+%7D++%5Bfrac%7Bln%5B%28lnx%2Be%5Ex%29%5D%7D%7B2sqrt%7Bx%7D%7D+++%2B+frac%7B1%7D%7Blnx%2Be%5Ex%7D+%2A%28+frac%7B+sqrt%7Bx%7D%7D%7Bx%7D%2B+e%5Ex%29++%5D "OTBET: y'=(lnx+e^x)^{ sqrt{x} } [frac{ln[(lnx+e^x)]}{2sqrt{x}} + frac{1}{lnx+e^x} *( frac{ sqrt{x}}{x}+ e^x) ]")
1)логарифмируем левую и правую часть функции:
2) упрощаем
3) берем производную от левой и правой частей функции
4) выражаем y'
Так как
то конечный ответ:
Интересные вопросы
Предмет: Математика,
автор: Jxxiexjej
Предмет: Алгебра,
автор: fklinton38
Предмет: Математика,
автор: ksenderr
Предмет: Физика,
автор: vanekvanek199
Предмет: История,
автор: Аноним