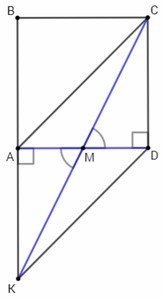
ПОМОГИТЕ ОВОЩУ! Точка M-середина стороны AD квадрата ABCD. Луч CM пересекает прямую AB в точке K. Докажите, что четырёхугольник ACDK является параллелограммом.

У квадрата все углы прямые, ∠A=∠D=90, ∠KAM=90
∠AMK=∠DMC (вертикальные углы), AM=DM
△AMK=△DMC (по острому углу и катету) =>
MK=MC
В четырехугольнике ACDK диагонали точкой пересечения делятся пополам => ACDK - параллелограмм.