Предмет: Геометрия, автор: Derye12

Высота правильной четырехугольной пирамиды равна 8 см, а боковое ребро 10 см Найдите апофему пирамиды

Ответы

Автор ответа: Hrisula
0

Ответ: √82 см

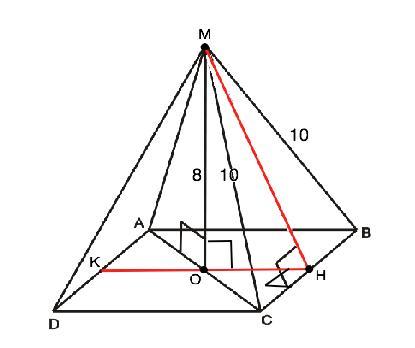
Объяснение: Вершина правильной четырехугольной пирамиды проецируется в центр основания - точку пересечения диагоналей квадрата. Пусть данная пирамида МАВСД, О - точка пересечения диагоналей основания. МО=8 - высота. МС=10 - боковое ребро, МН апофема ( высота боковой грани правильной пирамиды)

     Из прямоугольного треугольника МОС по т.Пифагора половина диагонали ОС=√(МC²-МО²)=√(100-64)=6 см

Тогда по т. о 3-х перпендикулярах ОН⊥ВС. ⇒ ∆ ОНС - прямоугольный, ОН=ОС•sin45°=6•√2/2=3√2 ⇒

МН=√(МО²+ОН²)=√(64+18)=√82 см

Приложения:
Предыдущий вопрос
Следующий вопрос
Интересные вопросы
Предмет: Алгебра, автор: fen1x212123
x+x-y привести подобные слогаемые
6 лет назад
Предмет: Другие предметы, автор: bavykinaarina
Почему большинство людей - правши?
​
6 лет назад
Предмет: Английский язык, автор: markaryanlola08
помогите пожалуйста!!!!​
6 лет назад
Предмет: Математика, автор: nazrin0503168692
десятичную дробь представленную в различной форме запишите в стандартной форме
9 лет назад
Предмет: Информатика, автор: zerozero2017
9) Запишите значение переменной s, полученное в результате работы следующей программы на языке программирования Паскаль.
Var s, i:integer;
Begin
S := 3;
For i := 2 to 5 do
S := S + 2*i;
Writeln(S);
end.

10) В таблице Sea хранятся данные о количестве россиян, отдыхавших на Черном море (Sea[1] - число россиян в 2001 году, Sea[2] - в 2002 и т.д.). Определите, какое число будет напечатано в результате работы следующей программы, написанной на языке программирования Паскаль.
Var k, s: integer;
Sea: array [1..12] of integer;
begin
Sea[] := 170; Sea[2] := 170;
Sea[3] := 190; Sea[4] := 210;
Sea[5] := 230; Sea[6] := 220;
Sea[7] := 240; Sea[8] := 160;
Sea[9] := 190; Sea[10] := 210;
Sea[11] := 170; Sea[12] := 170;
s := 100;
For k := 1 to 12 do
if Sea[k] > 220 then
begin
s := s + Sea[k];
end;
Writeln(s);
end.

5) Дан фрагмент электронной таблицы, в первой строке которой записаны числа, а
во второй – формулы.
СМ во вложение.





Какая из перечисленных ниже формул должна быть записана в ячейке C2, чтобы
построенная после выполнения вычислений круговая диаграмма по значениям
диапазона ячеек A2:D2 соответствовала рисунку?
диаграмма














1) =B1−1
2) =C1−D1+A1
3) =A1+D1+1
4) =D1*2+B1
9 лет назад