Предмет: Математика,
автор: Артёмммм01
помогите решить показательные уравнения
Приложения:
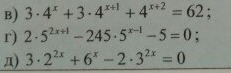
Ответы
Автор ответа:
0
В первом номере просто выносим за скобку множитель 
![4^x(3 + 3 cdot 4 + 4^2) = 62 \
4^x cdot 31 = 62 \
4^x = 2](https://tex.z-dn.net/?f=4%5Ex%283+%2B+3+cdot+4+%2B+4%5E2%29+%3D+62+%5C+%0A4%5Ex+cdot+31+%3D+62++%5C+%0A4%5Ex+%3D+2++ "4^x(3 + 3 cdot 4 + 4^2) = 62 \
4^x cdot 31 = 62 \
4^x = 2")
Во что надо возвести четверку, чтобы получить два? Очевидно, что это
. Но в общем случае, надо привести левую и правую часть к одному основанию
![displaystyle 2^{2 cdot x} = 2^1 \
2 cdot x = 1 \
x = frac{1}{2}](https://tex.z-dn.net/?f=displaystyle+2%5E%7B2+cdot+x%7D+%3D+2%5E1+%5C+%0A2+cdot+x+%3D+1++%5C+%0Ax+%3D++frac%7B1%7D%7B2%7D+ "displaystyle 2^{2 cdot x} = 2^1 \
2 cdot x = 1 \
x = frac{1}{2}")
Во втором случае, нужно немного преобразовать наше выражение и сделать замену переменных.
![2cdot 5cdot 5^{2x} - 49cdot 5cdot 5^{x-1} - 5 = 0 \
2cdot 5cdot 5^{2x} - 49cdot 5^{x} - 5 = 0 \
10cdot t^2 - 49cdot t - 5 = 0](https://tex.z-dn.net/?f=2cdot+5cdot+5%5E%7B2x%7D+-+49cdot+5cdot+5%5E%7Bx-1%7D+-+5+%3D+0++%5C+%0A2cdot+5cdot+5%5E%7B2x%7D+-+49cdot+5%5E%7Bx%7D+-+5+%3D+0+%5C+%0A10cdot+t%5E2+-+49cdot+t+-+5+%3D+0 "2cdot 5cdot 5^{2x} - 49cdot 5cdot 5^{x-1} - 5 = 0 \
2cdot 5cdot 5^{2x} - 49cdot 5^{x} - 5 = 0 \
10cdot t^2 - 49cdot t - 5 = 0")
Дальше остается решить квадратное уравнение, оставлю это на вас.
в 3 варианте используется следующий метод
Необходимо разделить уравнение либо на
либо на 
![displaystyle
3cdot 2^{2x} + 2^{x}cdot 3^{x} - 2cdot 3^{2x} = 0 \ \
3cdot frac{2^{2x}}{3^{2x}} + frac{2^xcdot 3^x}{3^{2x}} - 2 = 0 \ \
3cdot ( frac{2}{3} ) ^{2x} + (frac{2}{3} )^x - 2 = 0 \ \
t = (frac{2}{3})^x , t textgreater 0 \ \
3cdot t^2 + t - 2 = 0](https://tex.z-dn.net/?f=displaystyle+%0A3cdot+2%5E%7B2x%7D+%2B+2%5E%7Bx%7Dcdot+3%5E%7Bx%7D+-+2cdot+3%5E%7B2x%7D+%3D+0++%5C++%5C+%0A3cdot++frac%7B2%5E%7B2x%7D%7D%7B3%5E%7B2x%7D%7D+%2B++frac%7B2%5Excdot+3%5Ex%7D%7B3%5E%7B2x%7D%7D+-+2+%3D+0+%5C++%5C+%0A3cdot+%28+frac%7B2%7D%7B3%7D+%29+%5E%7B2x%7D+%2B++%28frac%7B2%7D%7B3%7D+%29%5Ex+-+2+%3D+0++%5C++%5C+%0At+%3D++%28frac%7B2%7D%7B3%7D%29%5Ex+%2C+t++textgreater+++0+%5C++%5C+%0A3cdot+t%5E2+%2B+t+-+2+%3D+0 "displaystyle
3cdot 2^{2x} + 2^{x}cdot 3^{x} - 2cdot 3^{2x} = 0 \ \
3cdot frac{2^{2x}}{3^{2x}} + frac{2^xcdot 3^x}{3^{2x}} - 2 = 0 \ \
3cdot ( frac{2}{3} ) ^{2x} + (frac{2}{3} )^x - 2 = 0 \ \
t = (frac{2}{3})^x , t textgreater 0 \ \
3cdot t^2 + t - 2 = 0")
Дальше опять квадратное уравнение. Только не забудьте сделать обратную замену!
Во что надо возвести четверку, чтобы получить два? Очевидно, что это
Во втором случае, нужно немного преобразовать наше выражение и сделать замену переменных.
Дальше остается решить квадратное уравнение, оставлю это на вас.
в 3 варианте используется следующий метод
Необходимо разделить уравнение либо на
Дальше опять квадратное уравнение. Только не забудьте сделать обратную замену!
Интересные вопросы
Предмет: История,
автор: dianka25012011
Предмет: Математика,
автор: ghfghfhfghfujghjgjgy
Предмет: Қазақ тiлi,
автор: rahmetollaevalihan
Предмет: Математика,
автор: Свк999
Предмет: Химия,
автор: SpaceCats