Предмет: Геометрия,
автор: David3154
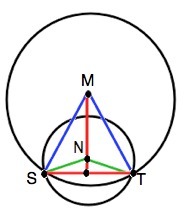
Окружности с центрами в точках M и N пересекаются в точках S и T,причём точки M и N лежат по одну сторону от прямой ST.Докажите что прямые MN и ST перпендикулярны.
Ответы
Автор ответа:
0
Концы хорды ST лежат на обеих окружностях.
Треугольники SMT и SNT равнобедренные, так как их боковые стороны - радиусы соответственно большей и меньшей окружностей.
В ∆ SMN и ∆ TMN стороны SM=MT; SN=NТ. MN- общая. Эти треугольники равны по 3-м сторонам.
Тогда ∠SМN=∠TMN, ⇒ MN- биссектриса угла SMT. В равнобедренном треугольнике биссектриса является ещё и медианой и высотой. Следовательно, MN и ST перпендикулярны.
Приложения:
Интересные вопросы
Предмет: Русский язык,
автор: alenalazarenko495
Предмет: Русский язык,
автор: Аноним
Предмет: Химия,
автор: bahon888999
Предмет: Алгебра,
автор: Аноним
Предмет: Математика,
автор: дианаЛи1