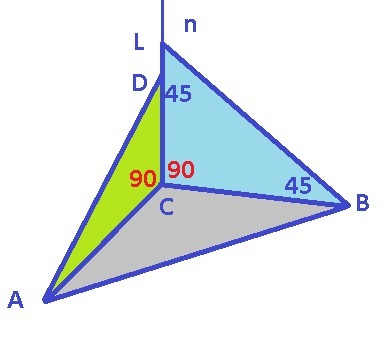
Через вершину C треугольника ABC проходит прямая n, которая не лежит в плоскости треугольника. На прямой n отмечены точки D и L так, что уголDAC+уголADC=90градусов, LC=BC и уголCLB=45градусов. Докажите, что прямая n перпендикулярна к плоскости ABC

Рисунок к задаче в приложении.
Сумма углов треугольника - равна 180°
РЕШЕНИЕ
1) ∠ACD = 180° - (∠DAC+ ∠ADC) = 180 - 90 = 90°
Вывод: прямая CD⊥AC.
2) LC=BC- треугольник равнобедренный.
∠CLB = ∠CBL = 45°
∠LCB = 180 - (45+45) = 90°
Вывод: прямая LC⊥CB.
Вывод: СL перпендикулярна двум прямым АС и ВС принадлежащим плоскости α, значит перпендикулярна всей плоскости α

Возможно надо добавить "школьные" слова.