Провести полное исследование функции и построить график:
f(x)=x^3/(1+x^2)

1.Область определения D(x) - непрерывная  Х∈(-∞;+∞).

Вертикальных асимптот - нет.

2. Пересечение с осью Х. Y=0 при х = 0. 

3. Пересечение с осью У.  У(0) = 0. 

4. Поведение на бесконечности.limY(-∞) = - ∞  limY(+∞) = +∞. 

Горизонтальных асимптот - нет.

5. Исследование на чётность.Y(-x) = - Y(x).

Функция нечётная. 

6. Производная функции.

Корень при Х=0. Схема знаков производной.

(-∞)__(>0)__(х=0)_(<0)__(+∞)

7. Локальные экстремумы. 

Максимума и минимума  – нет.

8. Интервалы монотонности. 

Возрастает на всем интервале определения- Х∈(-∞;+∞)

9. Вторая производная - Y"(x).

Корни производной - точки перегиба:  х1 = 0, х2= -√3, х3= √3. 

9. Выпуклая “горка» Х∈(-√3;0)∪√3;+∞), Вогнутая – «ложка» Х∈(-∞;-√3)∪(0;√3). 

10. Область значений Е(у) У∈(-∞;+∞) 

11. Наклонная асимптота. Уравнение: lim(∞)(k*x+b – f(x).  

k=lim(∞)Y(x)/x = x²/(1+x²) = 1. Уравнение: Y =x/ 

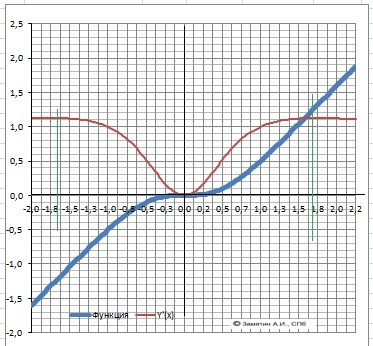
12.График в приложении.