Решите систему уравнений
{xy+8x-y=8
{x^2+y^2=10

Решим систему графически.

Первое уравнение раскладываем на множители

имеем две прямые x=1 и y=-8

Второе уравнение системы - уравнение окружности с центром в (0; 0) и радиусом √10≈3,2 (погрешность большой роли не сыграет)

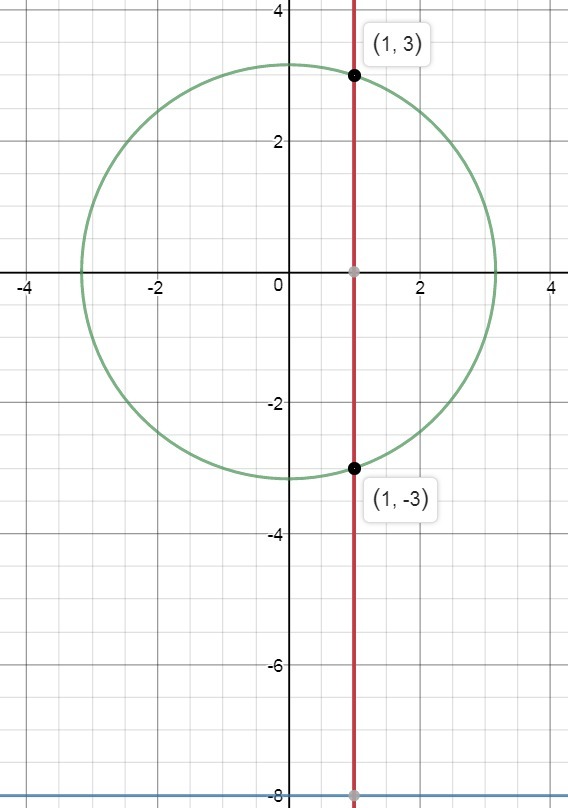
Выполняем построение графиков. Видно, что y=-8 окружность не пересекает, x=1 пересекает окружность в точках (1; 3) и (1; -3)

Ответ: (1; 3), (1; -3)

можно и не графически решить, просто подставив x=1, затем y=-8 во второе уравнение. Первый случай дает y=3, y=-3, второй - нет решений