Предмет: Математика, автор: HYFR

Исследуйте функцию и построить ее график

Приложения:

Ответы

Автор ответа: xERISx

$y = \frac{x^2+3}{x+1} \\ \\ y=x-1+ \frac{4}{x+1}$

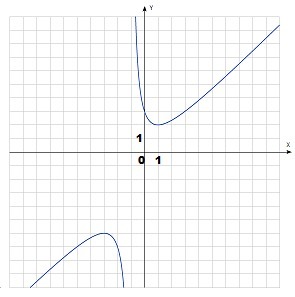
1) Область определения: x+1≠0  ⇒ x≠-1
D(f) = (-∞; -1)∪(-1;+∞)

2) Область значений (см. п. 6):
E(f) = (-∞; -6]∪[2; +∞)

3) Нули функции
$y = \frac{x^2+3}{x+1}; \frac{x^2+3}{x+1} =0$
x²=-3 ⇒ пересечений с осью ОХ нет.

4) Пересечение с осью OY
x=0 $y = \frac{x^2+3}{x+1}= \frac{0+3}{0+1} = 3$
Функция пересекает ось OY в точке (0; 3)

5) y>0; $\frac{x^2+3}{x+1}\ \textgreater \ 0$ при x+1>0;
x∈(-1; ∞)
y<0;   $\frac{x^2+3}{x+1}\ \textless \ 0$ при x+1<0;
x∈(-∞; -1)

6) Экстремумы
$y'=(x-1+ \frac{4}{x+1} )'=1+4*( \frac{1}{x+1} )'=1+4* \frac{-1}{(x+1)^2} \\ \\ y'=1- \frac{4}{(x+1)^2} = \frac{(x+1)^2-4}{(x+1)^2} \\ \\ \frac{(x+1)^2-4}{(x+1)^2} =0$
(x+1)²-4=0; (x+1)² = 4; x+1 = 2 или x+1 = -2
x₁ = 1; $y_1= \frac{1^2+3}{1+1} =2$
x₂ = -3;   $y_2= \frac{(-3)^2+3}{-3+1} =-6$
В точке x₁ = 1: y' меняет знак с минуса на плюс ⇒
(1; 2) - точка минимума
В точке x₂ = -3: y' меняет знак с плюса на минус ⇒
(-3; -6) - точка максимума

7) Функция убывает при x∈[-3; -1)∪(-1; 1]
Функция возрастает при x∈(-∞;-3]∪[1;+∞)

8) Функция не является периодической
$f(-x)= \frac{(-x)^2+3}{-x+1} = \frac{x^2+3}{-x+1}$
Функция не является четной.
Функция не является нечетной

9) вертикальная асимптота в точке разрыва x=-1
Левосторонний и правосторонний пределы бесконечны
$\lim_{x \to -1-0} (x-1+ \frac{4}{x+1}) =-1-1+ \frac{4}{-0} =-\infty \\ \\ \lim_{x \to -1+0} (x-1+ \frac{4}{x+1}) =-1-1+ \frac{4}{+0} =+\infty$
Наклонная асимптота y = kx + b
$k= \lim_{x \to б\infty} \frac{f(x)}{x} = \lim_{x \to б\infty} \frac{(x-1+ \frac{4}{x+1} )}{x} = \\ \\ =\lim_{x \to б\infty} (1- \frac{1}{x}+ \frac{4}{x(x+1)} )=1$

$b=\lim_{x \to б\infty} (f(x)-1*x)=\lim_{x \to б\infty} (x-1+ \frac{4}{x+1}-x )= \\ \\ =\lim_{x \to б\infty} (-1+ \frac{4}{x+1} )=-1$
Уравнение наклонной асимптоты
y=x-1

10)
$y'' = (1- \frac{4}{(x+1)^2} )'=- \frac{4*(-2)}{(x+1)^3} = \frac{8}{(x+1)^3}$
y''>0; $\frac{8}{(x+1)^3}\ \textgreater \ 0$ при x>-1
⇒ график функции вогнутый при x∈(-1; +∞)
y''<0;   $\frac{8}{(x+1)^3} \ \textless \ 0$ при x<-1
⇒ график функции выпуклый при x∈(-∞; -1)

Приложения: