В трапеции ABCD основания AD и BC относятся как 3:2, а сумма углов при основании AD равна 90градусов . Найдите радиус окружности, проходящей через точки A и B и касающейся прямой CD, если AB=3.

В трапеции ABCD основания AD и BC относятся как 3:2, а сумма углов при основании AD равна 90°. Найдите радиус окружности, проходящей через точки A и B и касающейся прямой CD, если AB = 3.

===========================================================

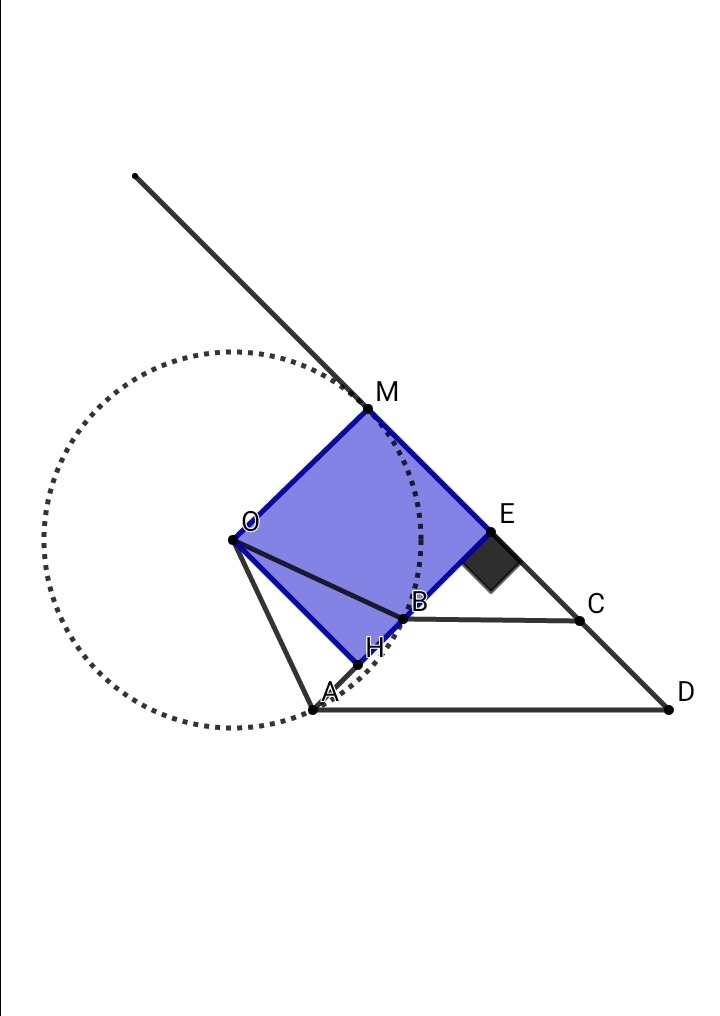
Продолжения боковых рёбер трапеции пересекаются в точке Е и образуют прямоугольный треугольник АЕD, ∠EAD + ∠EDA = 90° - по условию

ΔBCE подобен ΔAED по двум углам (∠AED - общий, ∠ЕВС = ∠EAD - как соответственные углы при BC || AD и секущей АВ)

BC/AD = BE/AE  ;  2/3 = BE/(AB + BE)

2/3 = BE/(3 + BE)  ⇒  6 + 2BE = 3BE ⇒ BE = 6

▪Радиус, проведённый в точку касания, перпендикулярен касательной  ⇒  OM⊥DM

▪Радиус, перпендикулярный хорде, делит её пополам ⇒ OH⊥AB, AH = HB = AB/2 = 3/2 = 1,5

В четырёхугольнике ОМЕН все углы прямые ⇒ ОМЕН - прямоугольник.

Значит, НЕ = ОМ = R = HB + BE = 1,5 + 6 = 7,5

ОТВЕТ: R = 7,5