Помогите решить задачу. Даю 50 баллов!!!

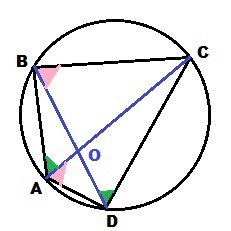
Четырехугольник ABCD вписан в окружность.
Дано:   AB:CD = 1:2  и  BD:AC = 2:3    
Найти:   AD:BC

ΔABO и ΔCDO
∠AOB = ∠DOC   - вертикальные углы
∠BAC = ∠BDC  -  вписанные углы опираются на одну дугу CB
⇒  ΔABO ~ ΔCDO  по двум равным углам.
AB : CD = 1 : 2     ⇒

⇒  OD = 2AO;   OC = 2BO

AC = AO + OC = AO + 2BO
BD = BO + OD = BO + 2AO

По условию  BD : AC = 2 : 3   ⇒

3(BO + 2AO) = 2(AO + 2BO)
3BO + 6AO = 2AO + 4BO
4AO = BO    ⇒     AO : BO = 1 : 4

ΔAOD и ΔBOC
∠AOD = ∠BOC  - вертикальные углы
∠CBD = ∠DAC  - вписанные углы опираются на одну дугу CD ⇒
ΔAOD ~ ΔBOC  по двум равным углам   ⇒


Ответ:   AD : BC = 1 : 4