Предмет: Алгебра, автор: Аноним

Найти критические точки на указанном промежутке

Приложения:

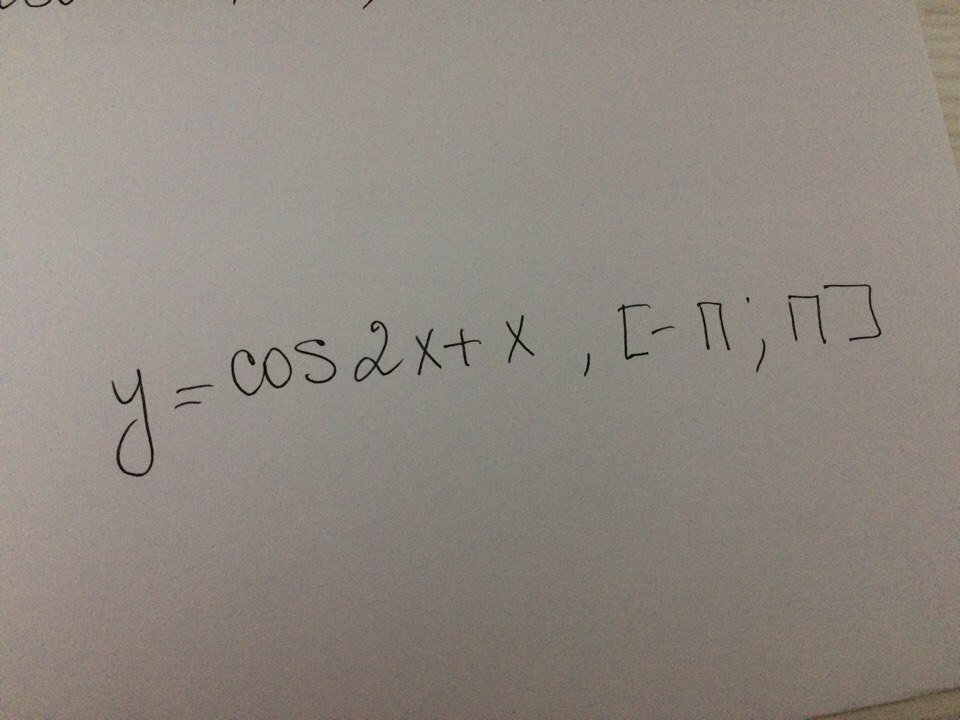
Ответы

Автор ответа: Эксперт5

$y=cos2x+x\; \; \; [- \pi ; \pi ]\\y`(x)=(cos2x+x)`=-2sin2x+1\\y`(x)=0\\-2sin2x+1=0\\-2sin2x=-1\\sin2x=1/2\\\\2x_1= \pi /6+ \pi n, n\in Z\\x_1= \pi /12+ \pi n/2, n\in Z\\\\2x_2=5 \pi /6+ \pi n, n\in Z\\x_2=5 \pi /12+ \pi n/2, n\in Z$

$[- \pi ; \pi ]\\\\x_1= \pi /12+ \pi n/2, n\in Z\\n=0\; \;\; \; x= \pi /12\\n=1\; \; \; \; x= \pi /12+ \pi /2= \pi /12+6 \pi /12=7 \pi /12\\n=-1\; \; \; \; x= \pi /12- \pi /2= \pi /12-6 \pi /12=-5 \pi /12\\n=-2\; \; \; \; x= \pi /12- \pi = \pi /12-12 \pi /12=-11 \pi /12$

$x_2=5 \pi /12+ \pi n/2, n\in Z\\n=0\; \; \; \; x=5 \pi /12\\n=1\; \; \; \; x=5 \pi /12+ \pi /2=5 \pi /12+6 \pi /12=11 \pi /12\\n=-1\; \; \; x=5 \pi /12- \pi /2=5 \pi /12-6 \pi /12=- \pi /12\\n=-2\; \; \; x=5 \pi /12- \pi =5 \pi /12-12 \pi/12=-7 \pi /12$

Аноним: Спасибо огромное

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Химия, автор: freescum408

які кристалічні ґратки у найбільш тугоплавких речовин?

6 лет назад

Предмет: Математика, автор: Rika08

log 9 ,log3 27 помогите пожалуста

6 лет назад

Предмет: Музыка, автор: ksuha080110

Как звучит сопровождение хора? какие инструменты придают музыке ощущение фантастики, колокольности устремлённости ввысь? В каком Ладу звучит музыка этой части?