Предмет: Геометрия, автор: ritka27

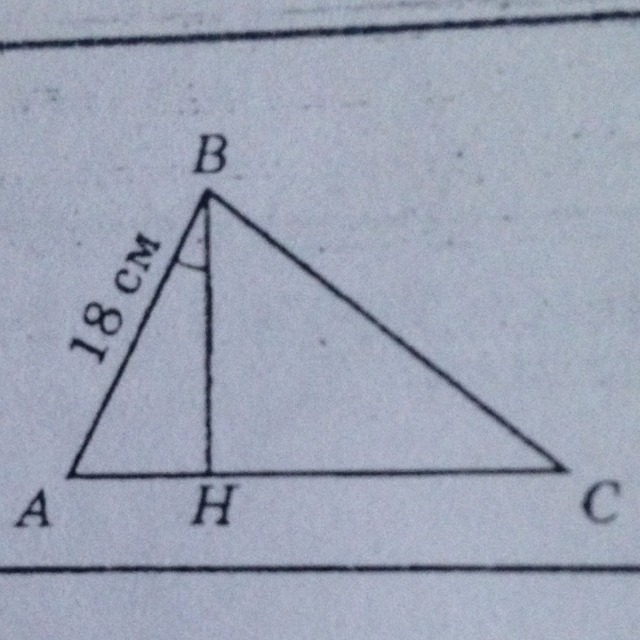
По данным рисунка найдите высоту треугольника АВС.Отмеченный угол равен 45°

Приложения:

Ответы

Автор ответа: Tanda80

Треугольник АВН - прямоугольный, т.к. ВН - высота.
В треугольнике АВН, искомая высота ВН, является катетом прилежащим у углу в 45°, а АВ=18 см - гипотенуза.
По определению функции косинус острого угла имеем:
сos(45°)=BH/AB. Откуда, ВН=АВ*сos(45°).
BH=18*(√2/2)=9√2 (см).

SergeyTishkin: а можно вторым способом решить?

Tanda80: думаю, что нет. А там кто его знает, может и можно. :)

SergeyTishkin: да, все не надо, спасибо я сам нашел через теорему пифагора

Tanda80: ну, через теорему Пифагора можно, но сначала все равно надо будет найти один из катетов, а точнее противолежащий углу 45°.

SergeyTishkin: не обязательно, треугольник abh - равнобедренный получается, значит катеты равны, а потом просто по формуле находим каждый катет

SergeyTishkin: просто по чертеду не понятно, нам учитель сказал что вторым способом чертеж неверен будет

Tanda80: это через х решать получается. Тоже в принципе, можно.

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: История, автор: liana286

1. Как соотносились между собой теология и философия?
2. Почему именно собор стал наиболее ярким воплощением средневековой архитектуры? СРОЧНО!!!! и кратко ! ПОЖАЛУЙСТА!!!!!!