В сферу радиуса R вписан цилиндр, диагональ осевого сечения которого составляет с образующей угол а. Найти:а)радиус цилиндра, б)объем цилиндра

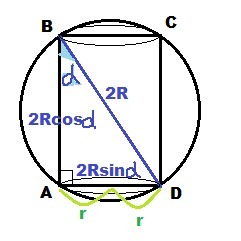
Осевое сечение цилиндра с образующей AB - прямоугольник ABCD с диагональю BD, равной двум радиусам сферы:
BD = 2R. 
AВ = 2r  -  два радиуса цилиндра; AB - высота цилиндра h

ΔBAD - прямоугольный, ∠BAD = 90°, ∠ABD = α
AD = 2r = 2R * sin α   ⇒  r = Rsin α
AB = h = 2R * cos α 

Объем цилиндра
V = S₀h = πr²h = π*(Rsin α)² * 2R*cos α = 2πR³sin²α*cosα
V = 2πR³(cos α - cos³α)

Ответ:  r = Rsin α    V=2πR³sin²α*cosα