Предмет: Алгебра,
автор: AripovZ
ПОМОГИТЕ ПОЖАЛУЙСТА С АЛГЕБРОЙ!!!НУЖНО СРОЧНО!!!
Приложения:
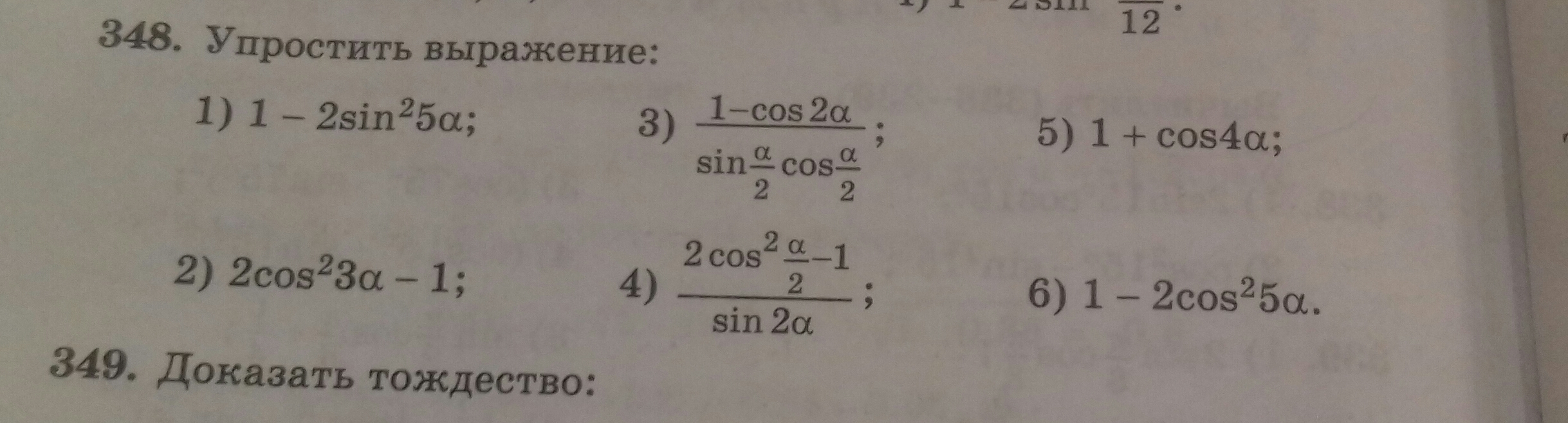
Ответы
Автор ответа:
2
1) косинус двойного угла

2) тоже косинус двойного угла

формула косинуса двойного угла:

3) формула произведения синуса на косинус


4)формула косинуса половинного аргумента


5)

6)

2) тоже косинус двойного угла
формула косинуса двойного угла:
3) формула произведения синуса на косинус
4)формула косинуса половинного аргумента
5)
6)
Интересные вопросы