Предмет: Математика, автор: Mimik197

Помогите пожалуйста исследовать полностью функцию и построить график.

Приложения:

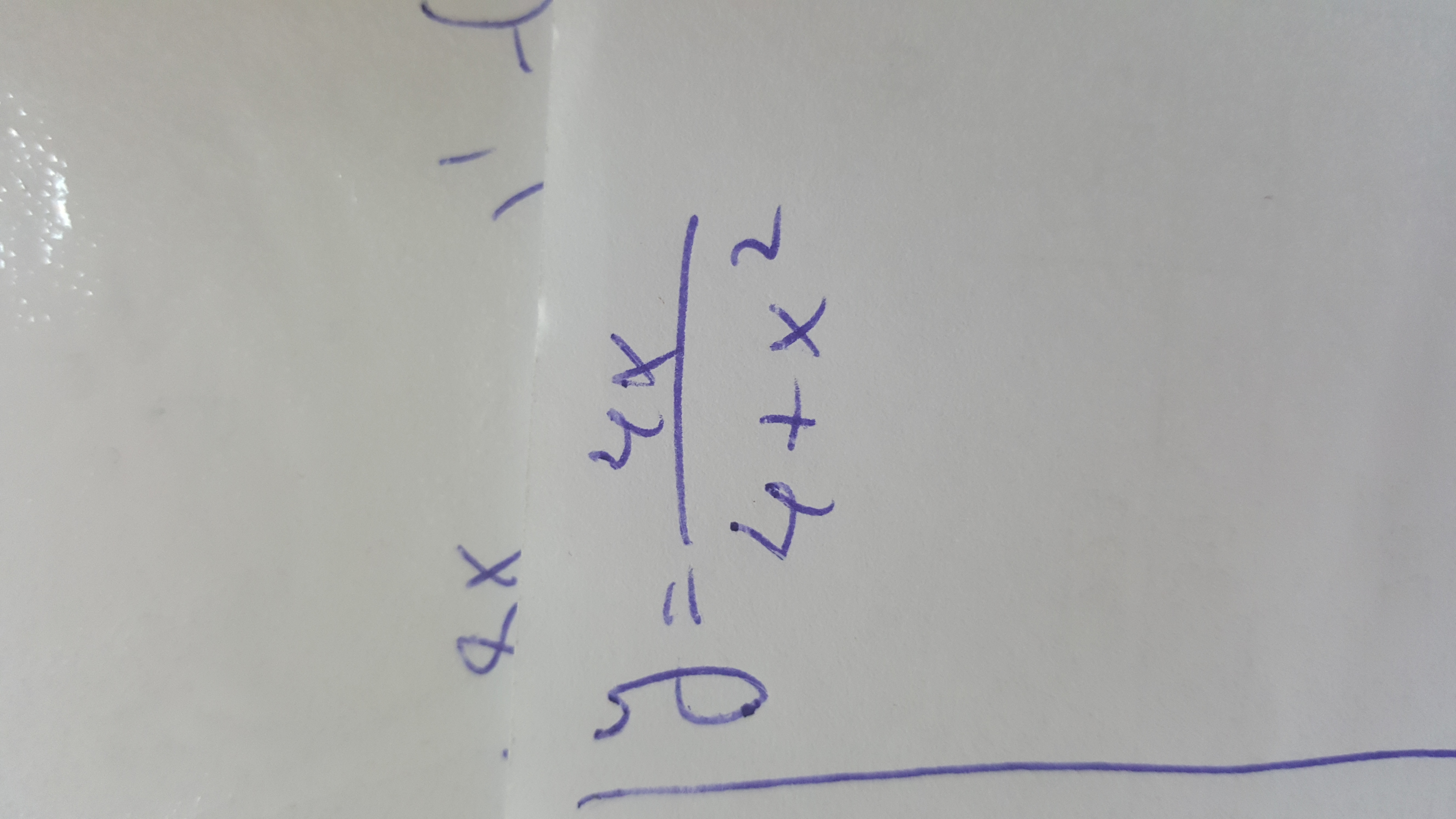
Ответы

Автор ответа: Vladislav006

Исследовать функцию и построить график $y= \frac{4x}{4+ x^{2}}$

Решение
1) Область определения функции.
Функция определена на всей числовой оси, то есть $x \in R$

2) Точки пересечения графика функции с осями
С осью Ох (у=0)
$\frac{4x}{4+ x^{2}} = 0 \Rightarrow x =0$
График имеет единственную точку пересечения и проходит через начало координат (0;0)

3) Исследуем функции на четность
$y (-x)= \frac{4(-x)}{4+ (-x)^{2}} = - \frac{4x}{4+ x^{2}}$
Так как
$y(-x) = - f(x)$ - то функция является нечетной

4) Функция не имеет точек разрыва, поэтому вертикальных асимптот нет.

Найдем наклонные асимптоты $y = k*x + b$ , где
$k = \lim_{x \to \pm \infty} \frac{f(x)}{x} = \lim_{x \to \pm \infty} \frac{4x}{x(4+ x^{2})} = \frac{4}{\pm \infty} = 0$
Так как k=0, то наклонных асимптот нет, а есть горизонтальные

Найдем теперь коэффициент b
$b= \lim_{x \to \infty} [f(x)-kx] = \lim_{x \to \infty} [\frac{4x}{4+ x^{2}} -0] = \frac{0}{1} = 0$

Подставляем найденные коэффициенты в формулу y = kx + b, получаем, что y = 0 - горизонтальная асимптота.

5) Найдем экстремумы функции. Для это найдем производную y' и приравняем ее к нулю y' = 0
$y'=( \frac{4x}{4+ x^{2}})' = \frac{(4x)'(4+ x^{2} ) - 4x(4+ x^{2} )' }{(4+ x^{2} )^2} = \frac{16-4 x^{2} }{(4+ x^{2} )^2}$

$\frac{16-4 x^{2} }{(4+ x^{2} )^2} = 0 \\ \\ 16-4 x^{2} = 0 \\ \\ x^{2} =4 \ \Rightarrow \ x = \pm 2$
Получили две критические точки.

В точке экстремума (х=-2) производная меняет знак с "-" на "+" значит это точка минимума

В точке экстремума (х= 2) производная меняет знак с "+" на "-" значит это точка максимума.

6) Найдем точки перегиба. Для этого найдем вторую производную у'' и приравняем её к нулю y'' = 0
$y'' = ( \frac{16-4 x^{2} }{(4+ x^{2} )^2})' = \frac{8x^3-96x}{(4+ x^{2})^3}$

$\frac{8x^3-96x}{(4+ x^{2})^3} = 0$
Так как знаменатель всегда больше нуля, то
$8x^3-96x = 0 \\ \\ 8x( x^{2} -12) = 0 \\ \\ x=0 \ \ \bigcup \ \ x= \pm 2 \sqrt{3}$

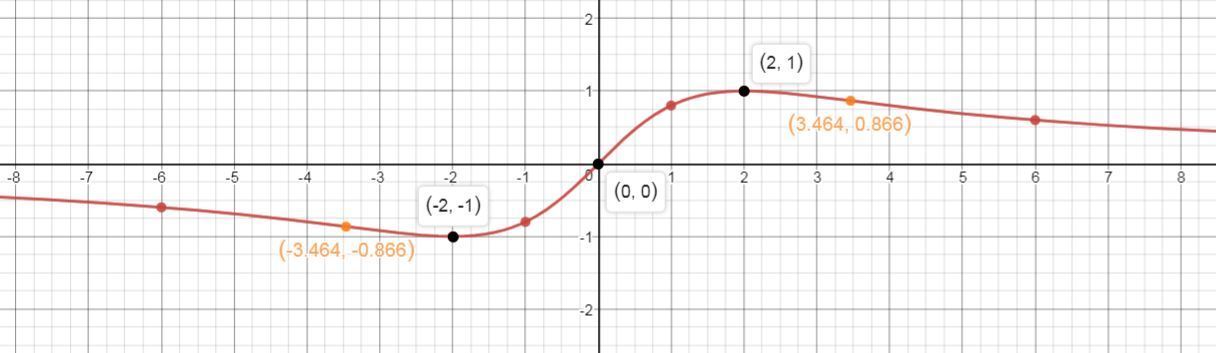
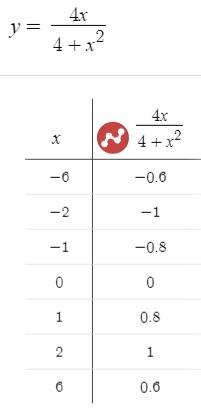
7) Построим график функции. Данные для построения и сам график, представлены ниже

Приложения: