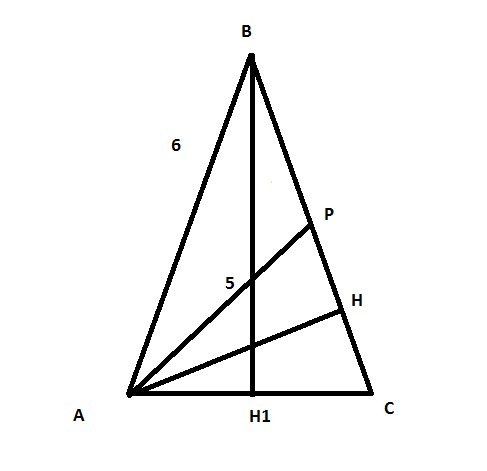
Отрезки AP и AH - соответсвенно медианы и высота равнобедренного треугольника ABC, основанием которого является отрезок AC. Известно, что AB=6 см, AP=5 см. Вычислите косинус угла PAH.

cos <PАH можно найти из прямоугольного ΔHAP, но пока в нем известна только одна сторона АР, поэтому найду еще вторую...
      Из ΔABP(в нем известны все стороны) найду cosB по т. косинусов
AP^2=AB^2+BP^2-2*AB*AP*cosB
5^2=6^2+3^2-2*6*3*cosB
25=45-36cosB
cosB=20/36=5/9
Теперь найду АС по этой же теореме
AC^2=6^2+6^2-2*6*6*5/9
AC^2=72-40=32
AC=4√2
AH1=AC/2=2√2
BH1^2=AB^2-AH1^2=6^2-(2√2)^2=36-8=28
AH=2√7
ΔABH1 и ΔACH подобны по 2 углам
AB/AC=BH1/AH
6/(4√2)=2√7/AH
AH=4√14/3
сos<PAH=AH/AP=4√14/(3*5)=4√14/15≈0.99