Предмет: Алгебра,
автор: полина1633
помогите очень срочно !!!
Приложения:
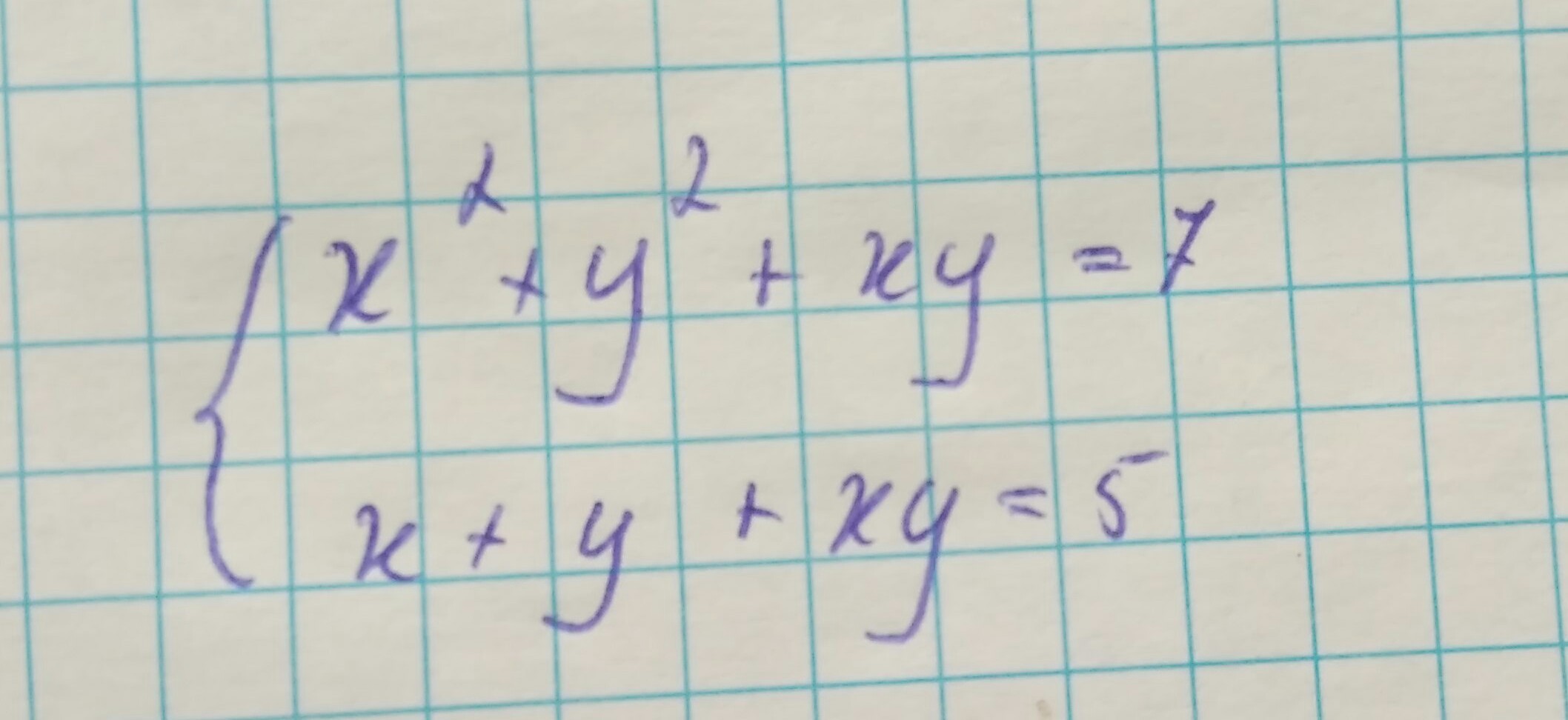
Ответы
Автор ответа:
1
{x²+y²+xy=7
{x+y+xy=5
{(x+y)²-2xy+xy=7
{x+y+xy=5
{(x+y)²-xy=7
{x+y+xy=5
-----------------
(x+y)²+(x+y)-12=0
D=49
1) x+y=(-1+7)/2=3 ⇒ x=3-y
2)x+y=(-1-7)/2=-4 ⇒ x=-4-y
x=3-y
3-y+y+(3-y)*y=5
3+3y-y²=5
y²-3y+2=0
D=1
y₁=(3-1)/2=1 x₁=3-1=2
y₂=(3+1)/2=2 x₂=3-2=1
x=-4-y
-4-y+y+(-4-y)*y=5
-4-4y-y²=5
y²+4y+9=0
D=16-36<0 нет корней
ответ (1;2) (2;1)
{x+y+xy=5
{(x+y)²-2xy+xy=7
{x+y+xy=5
{(x+y)²-xy=7
{x+y+xy=5
-----------------
(x+y)²+(x+y)-12=0
D=49
1) x+y=(-1+7)/2=3 ⇒ x=3-y
2)x+y=(-1-7)/2=-4 ⇒ x=-4-y
x=3-y
3-y+y+(3-y)*y=5
3+3y-y²=5
y²-3y+2=0
D=1
y₁=(3-1)/2=1 x₁=3-1=2
y₂=(3+1)/2=2 x₂=3-2=1
x=-4-y
-4-y+y+(-4-y)*y=5
-4-4y-y²=5
y²+4y+9=0
D=16-36<0 нет корней
ответ (1;2) (2;1)
Автор ответа:
1
делаем замены:
x+y=a
xy=b
также:

получим:

решим эту систему:

обратная замена:

2 решения: (1;2), (2;1)

2 система не имеет решений.
Ответ: (1;2), (2;1)
x+y=a
xy=b
также:
получим:
решим эту систему:
обратная замена:
2 решения: (1;2), (2;1)
2 система не имеет решений.
Ответ: (1;2), (2;1)
Интересные вопросы
Предмет: Информатика,
автор: RvanayaShirinka
Предмет: Геометрия,
автор: Mihail568
Предмет: Математика,
автор: leenara
Предмет: Математика,
автор: ойка1
Предмет: Математика,
автор: соня74343