Предмет: Алгебра, автор: 2001eka

(Очень срочно) Решите, пожалуйста, неравенство:

Приложения:

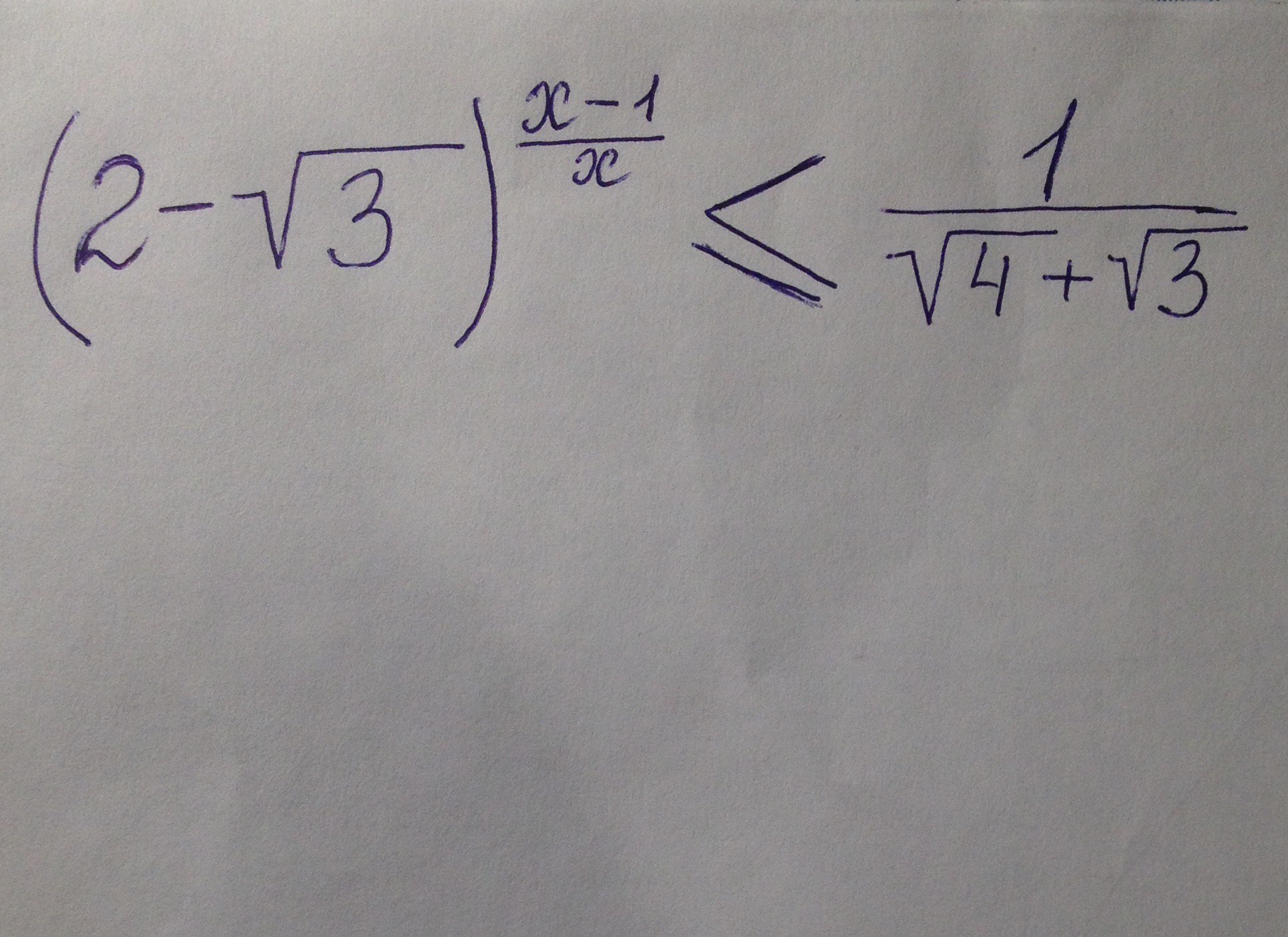
Ответы

Автор ответа: Tanda80

${(2 - \sqrt{3} )}^{ \frac{x - 1}{x} } \leqslant \frac{1}{ \sqrt{4} + \sqrt{3} }$
ОДЗ: х≠0.
${(2 - \sqrt{3} )}^{ \frac{x - 1}{x} } \leqslant \frac{1}{2 + \sqrt{3} }$
${(2 - \sqrt{3}) }^{ \frac{x - 1}{x} } \leqslant \frac{2 - \sqrt{3} }{(2 + \sqrt{3})(2 - \sqrt{3}) }$
${(2 - \sqrt{3}) }^{ \frac{x - 1}{x} } \leqslant \frac{2 - \sqrt{3} }{4 - 3}$
${(2 - \sqrt{3}) }^{ \frac{x - 1}{x} } \leqslant 2 - \sqrt{3}$
Последнее неравенство запишем в виде

${(2 - \sqrt{3}) }^{ \frac{x - 1}{x} } \leqslant {(2 - \sqrt{3} )}^{1}$

Т. к. √3 приблизительно равен 1,7, то 0<2-√3<1, а значит
$\frac{x - 1}{x} \geqslant 1$
$\frac{x - 1}{x} - 1 \geqslant 0$
$\frac{x - 1 - x}{x} \geqslant 0$
$\frac{ - 1}{x} \geqslant 0$
Т. к. значение дроби должно быть >=0, а числитель равен -1<0, то знаменатель х<0.
Ответ: х<0.

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Информатика, автор: dimadmitrii83

что это такое? я не пойму

6 лет назад

Предмет: Математика, автор: yasminsadykova52

ученик в первый день прочитал 30% всей книги, а второй 25% всей книги, а в третий остальную часть. покажите это на круговой диаграмме. помогите пожалуйста срочно нужно!!!!

6 лет назад

Предмет: История, автор: nlichnoe

ДАЮ 20 БАЛЛОВ
Сделайте четвёртый номер.

6 лет назад

Предмет: Математика, автор: Аноним

Буду очень ,вам благодарна ,если поможете разобраться ,заранее спасибо ,те кто хочет просто обсудить ,или написать ,что ребенок не хочет учиться ,пожалуйста даже не откликайтесь !!

9 лет назад

Предмет: Обществознание, автор: аленочка24

НАПИСАТЬ РЕКЛАМУ ПРО ШОКОЛАД

9 лет назад