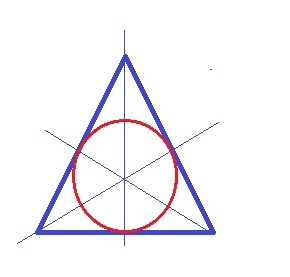
окружность касается всех сторон треугольника АВС. известно что точки касания являются серединами сторон треугольника. Вычислите длину радиуса окружности, если известно, что периметр треугольника АВС равен 16

РЕШЕНИЕ
Если касается в середине всех сторон треугольника, то это - равносторонний - правильный треугольник.
Из формулы периметра - Р = 3*а, находим 
а = Р/3 = 16/3 = 5 1/3 - сторона треугольника.
Радиус вписанной окружности в общем виде по формуле

Полупериметр - р = 3/2*а = 8
р-а = 2 2/3
Для правильного треугольника
r = a/(2√3)
Подставили значение стороны треугольника и преобразуем

или ≈ 1,54 - радиус - ОТВЕТ