Сечение сферы двумя параллельными плоскостями имеют длину 10 П и 24п. Найдите площадь поверхности сферы, если расстояние между параллельными плоскостями равно 7см и центры сечений лежат на одном радиус

Вообщем я немного упростила это решение

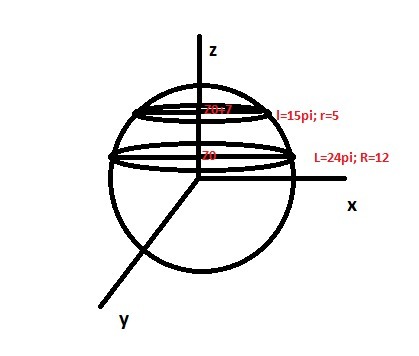
Пусть большее сечение лежит выше центра шара по оси Z , его радиус 12 и центр в точке (0;0;z0)

Тогда его уравнение будет x^2+y^2+z0^2=R^2

Здесь R радиус сферы. Так как радиус большего сечения 12(24pi/2pi), то уравнение большего круга

Будет 12^2+z0^2=R^2

Меньшее сечение x^2+y^2+(z0+7)^2==R^2; 25+z0^2+14z0+47=R^2

Вычитаю из первого второе , получу

119-17z0-49=0

-14z0=-70

Z0=5

Выходит большее сечение находится от центра шара по оси z на расстоянии 5, значит

R^2=5^2+12^2=169

R=13

S(cф)=4pi*13^2=676pi