Предмет: Математика, автор: ggggg85

даю 15 балов за решение

Приложения:

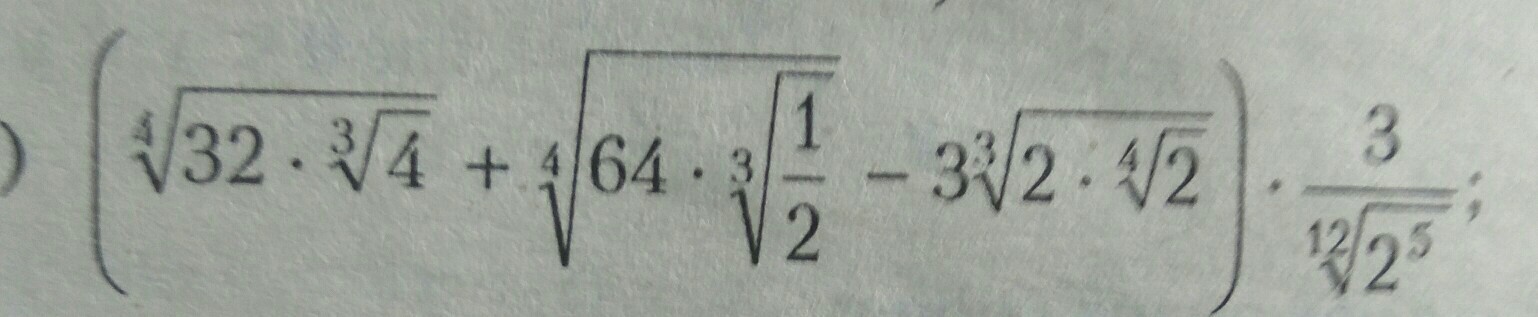
Artemkot123456789: Как

Artemkot123456789: Какой вопрос

Ответы

Автор ответа: MrsVaderr

$$$\Large \displaystyle ( \sqrt[4]{32 \cdot \sqrt [3] {4}}+ \sqrt [4] {64 \cdot \sqrt [3] { \frac{1}{2}}}- 3 \sqrt[3]{2 \cdot \sqrt[4]{2}}) \cdot \frac{3}{ \sqrt[12]{2^5}}=$
$$$\Large \displaystyle ((32 \cdot 4^{ \frac{1}{3}})^{ \frac{1}{4}} + (64 \cdot (\frac{1}{2})^{ \frac{1}{3}})^{ \frac{1}{4}}+3 \cdot (2 \cdot 2^{ \frac{1}{4}})^{ \frac{1}{3}}) \cdot$
$$$\Large \displaystyle \cdot \frac{3}{2^{\frac{5}{12}}}=((32^{\frac{1}{4}} \cdot 4^{ \frac{1}{12}}})+(64^{ \frac{1}{4}} \cdot (\frac{1}{2})^{\frac{1}{12}}})+3 \cdot 2^{ \frac{1}{3}}\cdot 2^{\frac{1}{12}}) \cdot \frac{3}{2^{\frac{5}{12}}}$
$$$\Large \displaystyle = ((2^{ \frac{5}{4}} \cdot 2^{ \frac{1}{6}}})+(2^{\frac{3}{2}} \cdot 2^{- \frac{1}{12}}})+3 \cdot 2^{ \frac{1}{3}} \cdot 2^{ \frac{1}{12}}) \cdot \frac{3}{2^{\frac{5}{12}}} =$
$$$\Large \displaystyle = ((2^{\frac{5}{4}+ \frac{1}{6}})+(2^{\frac{3}{2}- \frac{1}{12}})+3 \cdot 2^{ \frac{1}{3}+ \frac{1}{12}}) \cdot \frac{3}{2^{ \frac{5}{12}}}=$
$$$\Large \displaystyle = (2^{\frac{17}{12}}+2^{\frac{17}{12}}+3 \cdot 2^{\frac{5}{12}}) \cdot \frac{3}{2^{\frac{5}{12}}}= 2 \cdot \frac{3 \cdot 2^{\frac{17}{12}}}{2^{ \frac{5}{12}}}+ \frac{3 \cdot 3 \cdot 2^{ \frac{5}{12}}}{2^{\frac{5}{12}}}$
$$$\Large \displaystyle = {2 \cdot 3 \cdot 2^{\frac{12}{12}}}{}+ 3\cdot 3 = 3 \cdot 2 \cdot 2+ 3 \cdot 3 = 12+9 = 21$

Ответ: 21

ggggg85: спасибо, но смысла нет, если не понятно

mionkaf1: Как по мне - всё красиво и понятно.

ggggg85: можете научить расшифровывать?

mionkaf1: А у вас символы?

ggggg85: да

mionkaf1: Вы с телефона?

ggggg85: да

mionkaf1: Закройте приложение и откройте опять его, должно помочь, такое бывает

ggggg85: не работает (

ggggg85: попробую с пк