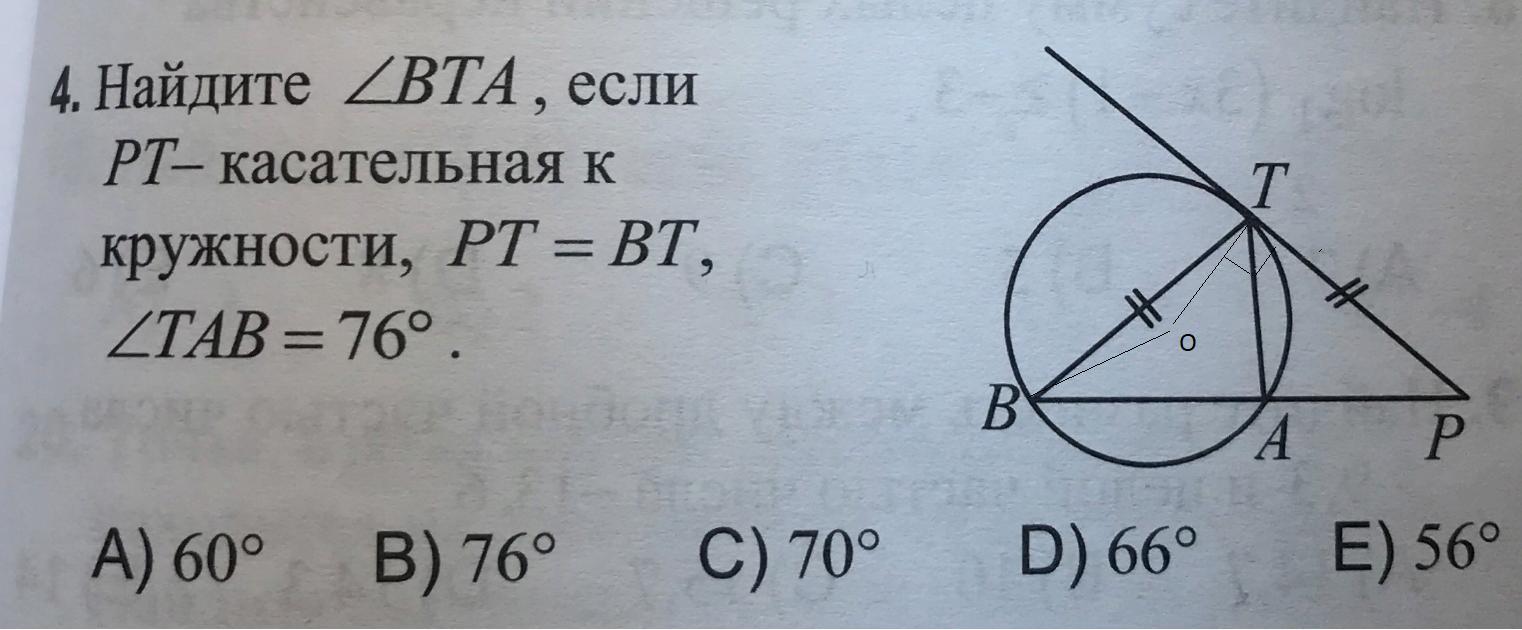
Найдите угол bTa , если PT касательная к окружности. PT=BT
Угол tAb=76 градусов

Пусть О-центр окружности, тогда ΔВОТ-равнобедренный -так как ВО=ОТ-радиусы этой окружности.

<BOT-центральный, опирается на дугу ВТ (не проходящую через точку А), на которую тоже опирается вписанный <TAB.Значит эта дуга ВТ равна 2*<ВАТ=2*76=152°.

Тогда на 2 одинаковых угла в этом треугольнике остается 180-152=28 градусов

<TBO=<BTO=(180-152)/2=14°

<OTP=90(т.к. ОТ-касательная)

<BTP=<BTO+<OTP=14+90=104

В Δ ВТР <B=<P=(180-<BTP)/2=(180-104)/2=76/2=38

В ΔВТА <BTA=180-<B-<A=180-38-76=66