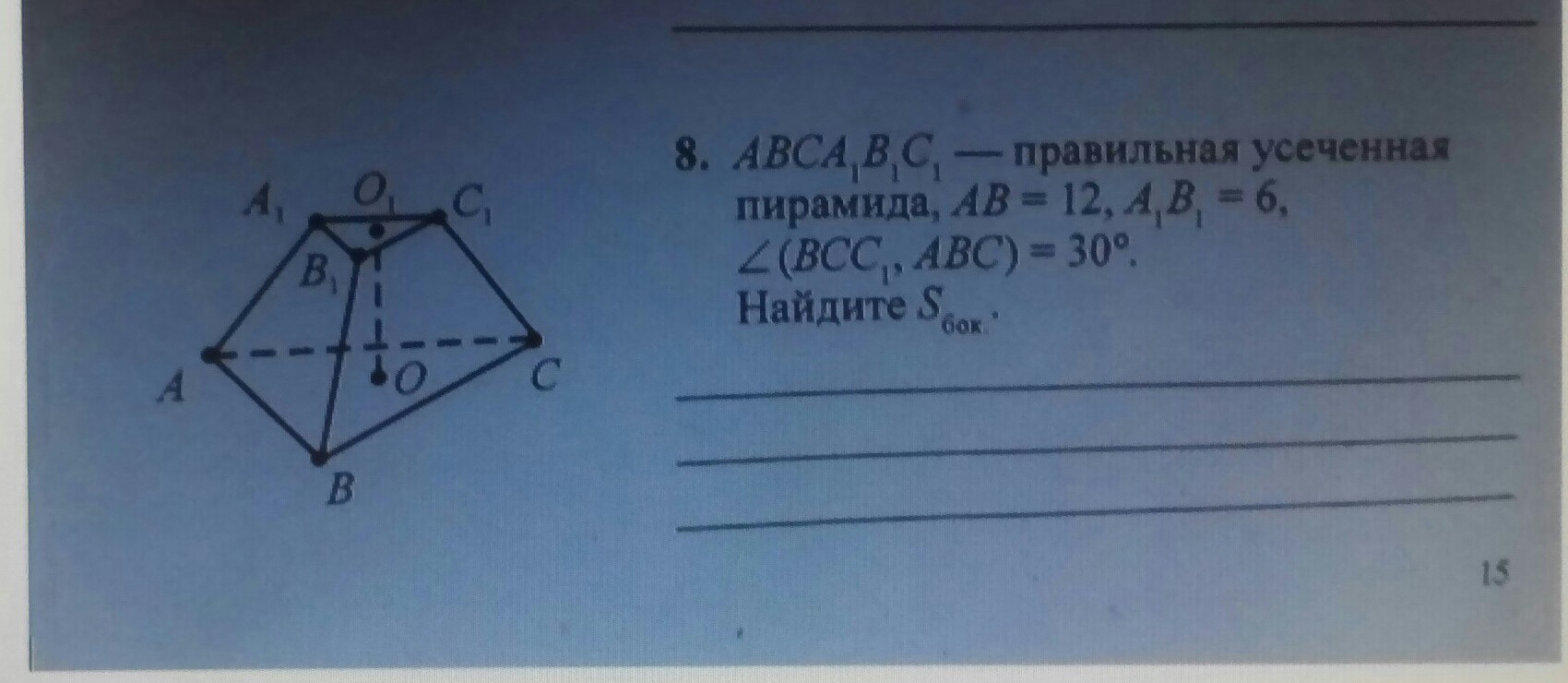
решите геометрию(#8) пожалуйста

Боковая поверхность состоит из 3 одинаковых равнобедренных трапеций, у которых известны основания, но неизвестны высоты...
Поэтому если я найду высоту одной такой трапеции-задача будет решена..
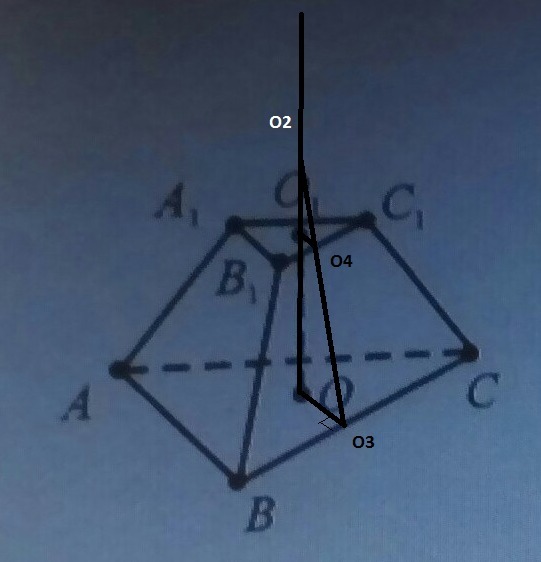
Рассмотрю ΔOO2O3-прямоугольный, <O3=30 по условию
Меня интересует О3О4-это высота трапеции, которая мне нужна
ΔO2O1O4 и ΔО2ОО3-подобны, поэтому О3О4=О2О3-О2О4, которые я найду из подобных треугольников
ОО3 и О1О4-радиусы вписанных окружностей в равносторонние треугольники
О1О4=6/√3=2√3; OO3=12/√3=4√3
k=O1O4/OO3=4√3/(2√3)=2- коэффициент подобиятреугольников
О3О2=ОО3/cos30=4√3/(√3/2)=8
O3O4=O3O2/k=8/2=4
Высота трапеции найдена , нахожу ее площадь
S=O3O4*(AB+A1B2)/2=4*(12+6)/2=4*9=36
S(бок)=3S=3*36=108