Предмет: Алгебра,
автор: xsanek19931024p62iye
Здравствуйте! Дана такая задача. Не могу понять, как это нужно делать. Сижу разбираюсь, но пока не могу догнать. Исследовать функцию y = g(x) методами дифференциального исчисления и построить её график.
Приложения:
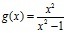
Ответы
Автор ответа:
1
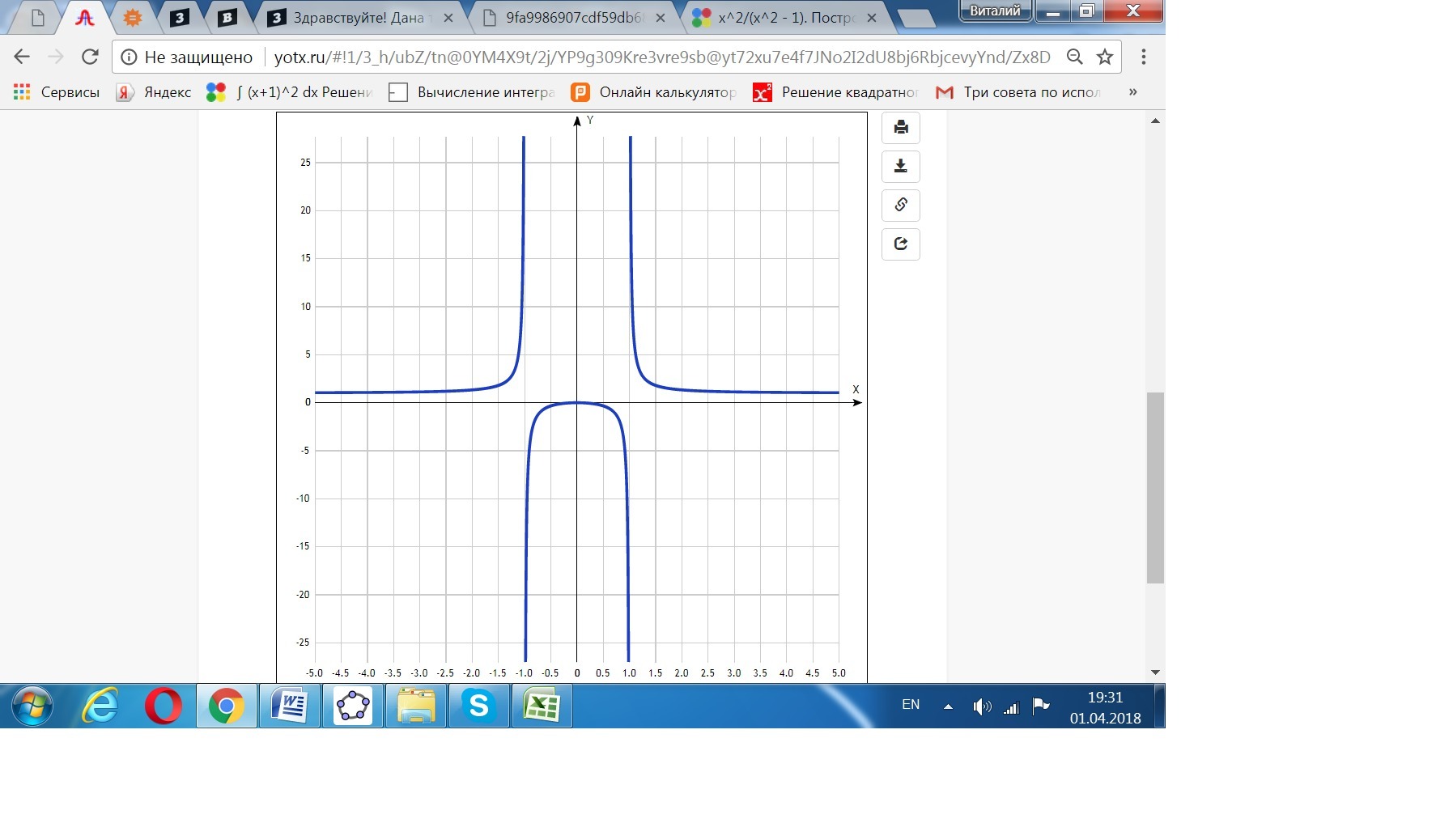
Дана функция х²/(х² - 1).
Точки, в которых функция точно не определена, определяются, если знаменатель разложить на множители: х²/((х + 1)(х - 1)).
x₁ = -1.
x₂ = 1.
График функции пересекает ось X при f = 0
значит надо решить уравнение:
x²/(x² - 1) = 0.
Решением этого уравнения есть х = 0. Точка (0; 0).
График пересекает ось Y, когда x равняется 0:
подставляем x = 0 в x^2/(x^2 - 1). Это та же точка (0; 0).
Для того, чтобы найти экстремумы, нужно решить уравнение
d/d x f(x ) = 0.
(производная равна нулю),
и корни этого уравнения будут экстремумами данной функции.
Первая производная равна: y' = -2x/((x² - 1)²).
Отсюда видно, что производная равна 0 только в точке х= 0.
При исследовании функции на экстремум находится производная, приравнивается к 0, найденные точки выставляются на числовой прямой; к ним добавляются те точки, в которых производная не определена. На промежутках находят знаки производной. Где производная положительна - функция возрастает, где отрицательна - там убывает. Точки, в которых происходит смена знака и есть точки экстремума - где производная с плюса меняется на минус - точка максимума, а где с минуса на плюс - точки минимума.
С учётом разрыва функции в точках х=1 и х=-1 получили 4 промежутка монотонности: (-∞; -1), (-1; 0), (0; 1) и (1; +∞).
x = -2 -1 -0,5 0 0,5 1 2
y' = 0,4444 - 1,7778 0 -1,7778 - -0,4444.
Имеем 1 локальный максимум х = 0.
Промежутки возрастания (-∞; -1) и (-1; 0).
убывания (0; 1) и (1; +∞).
Функция чётная.
Точки, в которых функция точно не определена, определяются, если знаменатель разложить на множители: х²/((х + 1)(х - 1)).
x₁ = -1.
x₂ = 1.
График функции пересекает ось X при f = 0
значит надо решить уравнение:
x²/(x² - 1) = 0.
Решением этого уравнения есть х = 0. Точка (0; 0).
График пересекает ось Y, когда x равняется 0:
подставляем x = 0 в x^2/(x^2 - 1). Это та же точка (0; 0).
Для того, чтобы найти экстремумы, нужно решить уравнение
d/d x f(x ) = 0.
(производная равна нулю),
и корни этого уравнения будут экстремумами данной функции.
Первая производная равна: y' = -2x/((x² - 1)²).
Отсюда видно, что производная равна 0 только в точке х= 0.
При исследовании функции на экстремум находится производная, приравнивается к 0, найденные точки выставляются на числовой прямой; к ним добавляются те точки, в которых производная не определена. На промежутках находят знаки производной. Где производная положительна - функция возрастает, где отрицательна - там убывает. Точки, в которых происходит смена знака и есть точки экстремума - где производная с плюса меняется на минус - точка максимума, а где с минуса на плюс - точки минимума.
С учётом разрыва функции в точках х=1 и х=-1 получили 4 промежутка монотонности: (-∞; -1), (-1; 0), (0; 1) и (1; +∞).
x = -2 -1 -0,5 0 0,5 1 2
y' = 0,4444 - 1,7778 0 -1,7778 - -0,4444.
Имеем 1 локальный максимум х = 0.
Промежутки возрастания (-∞; -1) и (-1; 0).
убывания (0; 1) и (1; +∞).
Функция чётная.
Приложения:
Интересные вопросы
Предмет: Окружающий мир,
автор: MiniChekFIRE
Предмет: Математика,
автор: nastyamelya2009
Предмет: Геометрия,
автор: alyasemenova2
Предмет: Химия,
автор: elminakowa2904