Предмет: Математика, автор: Vafim343348

помогите решить методом иррациональных функций

Приложения:

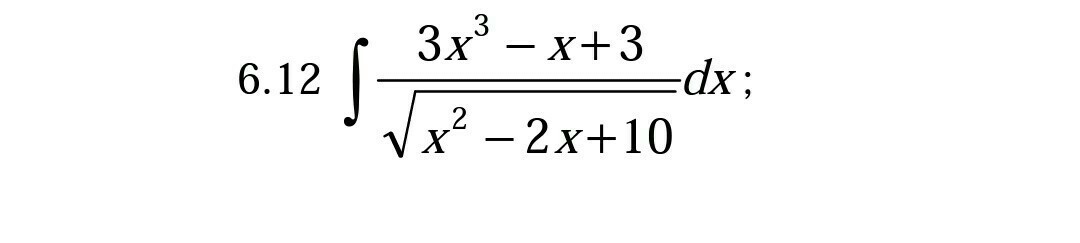
Vafim343348: ? где ответ

Аноним: нинаю

Ответы

Автор ответа: Alexаndr

Весьма интересный интеграл, значится и решать будем его нестандартно.
Для начала пару преобразований:
$\displaystyle\frac{3x^3-x+3}{\sqrt{x^2-2x+10}}=\frac{3x^3-x+3\sqrt{x^2-2x+10}}{x^2-2x+10}=\\=3(x+2)\sqrt{x^2-2x+10}-19\frac{x+3}{\sqrt{x^2-2x+10}}$

$\displaystyle3\int(x+2)\sqrt{x^2-2x+10}dx=\frac{3}{2}\int(2x-2+6)\sqrt{x^2-2x+10}dx=\\=\frac{3}{2}\int\sqrt{x^2-2x+10}d(x^2-2x+10)+9\int\sqrt{x^2-2x+10}dx=\\=\sqrt{(x^2-2x+10)^3}+\frac{9}{2}(x-1)\sqrt{x^2-2x+10}+\\+\frac{81}{2}ln|x-1+\sqrt{x^2-2x+10}|+C$

$-19\displaystyle\int\frac{x+3}{\sqrt{x^2-2x+10}}dx=-\frac{19}{2}\int\frac{2x-2+8}{\sqrt{x^2-2x+10}}dx=\\=-\frac{19}{2}\int\frac{d(x^2-2x+10)}{\sqrt{x^2-2x+10}}-76\int\frac{d(x-1)}{\sqrt{(x-1)^2+9}}=\\=-19\sqrt{x^2-2x+10}-76ln|x-1+\sqrt{x^2-2x+10}|+C$

$\displaystyle\int\frac{3x^3-x+3}{\sqrt{x^2-2x+10}}dx=\sqrt{(x^2-2x+10)^3}+\frac{9}{2}(x-1)\sqrt{x^2-2x+10}+\\+\frac{81}{2}ln|x-1+\sqrt{x^2-2x+10}|-19\sqrt{x^2-2x+10}-\\-76ln|x-1+\sqrt{x^2-2x+10}|+C=\sqrt{(x^2-2x+10)^3}+\\+\frac{1}{2}(9x-47)\sqrt{x^2-2x+10}-\frac{71}{2}ln|x-1+\sqrt{x^2-2x+10}|+C$
Проверка:
$\displaystyle(\sqrt{(x^2-2x+10)^3}+\frac{1}{2}(9x-47)\sqrt{x^2-2x+10}-\\-\frac{71}{2}ln|x-1+\sqrt{x^2-2x+10}|)'=\\\\=3\sqrt{x^2-2x+10}(x-1)+\frac{9}{2}\sqrt{x^2-2x+10}+\frac{(x-1)(9x-47)}{2\sqrt{x^2-2x+10}}-\\-\frac{71}{2\sqrt{x^2-2x+10}}=(3x+\frac{3}{2})\sqrt{x^2-2x+10}+\frac{9x^2-56x-24}{2\sqrt{x^2-2x+10}}=\\=\frac{3x^3-x+3}{\sqrt{x^2-2x+10}}$

Чтобы потом не было вопросов, что откуда я взял:
$\displaystyle\int\frac{dx}{\sqrt{x^2-2x+10}}=\int\frac{d(x-1)}{\sqrt{x^2-2x+1+9}}=\int\frac{d(x-1)}{\sqrt{(x-1)^2+9}}=\\=ln|x+1+\sqrt{(x-1)^2+9}|+C=ln|x+1+\sqrt{x^2-2x+10}|+C$
"Длинный логарифм"

$\displaystyle\int\sqrt{x^2-2x+10}dx=x\sqrt{x^2-2x+10}-\\-\int\frac{x^2-2x+10+x-10}{\sqrt{x^2-2x+10}}dx=x\sqrt{x^2-2x+10}-\\-\int\sqrt{x^2-2x+10}dx-\frac{1}{2}\int\frac{2x-2-18}{\sqrt{x^2-2x+10}}dx\\\\2\int\sqrt{x^2-2x+10}=x\sqrt{x^2-2x+10}-\int\frac{d(x^2-2x+10}{2\sqrt{x^2-2x+10}}+\\+9\int\frac{d(x-1)}{\sqrt{(x-1)^2+9}}\\\\2\int\sqrt{x^2-2x+10}=x\sqrt{x^2-2x+10}-\sqrt{x^2-2x+10}+\\+9ln|x-1+\sqrt{x^2-2x+10}|\\\int\sqrt{x^2-2x+10}=\frac{1}{2}((x-1)\sqrt{x^2-2x+10}+\\+9ln|x-1+\sqrt{x^2-2x+10}|)+C$
$\displaystyle u=\sqrt{x^2-2x+10};du=\frac{x-1}{\sqrt{x^2-2x+10}}\\dv=dx;v=x$

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Алгебра, автор: mcivenko54

30z2+2=(3z+1)(10z+3).

Ответ:
Помогите пожалуйста

6 лет назад

Предмет: Алгебра, автор: natazubchenko41

(7p+g)(49p^ 2 -7pg+g^ 2 )

6 лет назад

Предмет: Русский язык, автор: Nastya446688

Помогите пожалуйста Срочно!!!

6 лет назад