Предмет: Математика,
автор: SyrexMinus
Найдите область определения функции √(x^2+1)/(x^2−9).
Пожалуйста, объясните максимально подробно, ибо я глупый, как валенок.
Приложения:
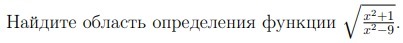
Ответы
Автор ответа:
1
Подкоренное выражение должно быть неотрицательным (больше или равно 0 ). Знаменатель дроби должен быть отличен от 0 .
Решаем методом интервалов.

Решаем методом интервалов.
SyrexMinus:
Куда делся делитель x^2+1 и почему >= превратился в >
x^2+1 никуда не делся, просто он не равен 0, он > 0 . Эта дробь не может = 0 (числитель не = 0 ). В точках х=-3 и х=3 функция не существует, т.к. при х=-3 и х=3 знаменатель обращается в 0, поэтому эти точки не входят в ООФ.
Интересные вопросы
Предмет: История,
автор: feretayn
Предмет: Английский язык,
автор: Аноним
Предмет: Химия,
автор: thecharmofevil
Предмет: Математика,
автор: 12345853
Предмет: Математика,
автор: Полина12314