Предмет: Алгебра, автор: birkovskiyyjoker

Помогите сделать 10 задание(полное решение)

Приложения:

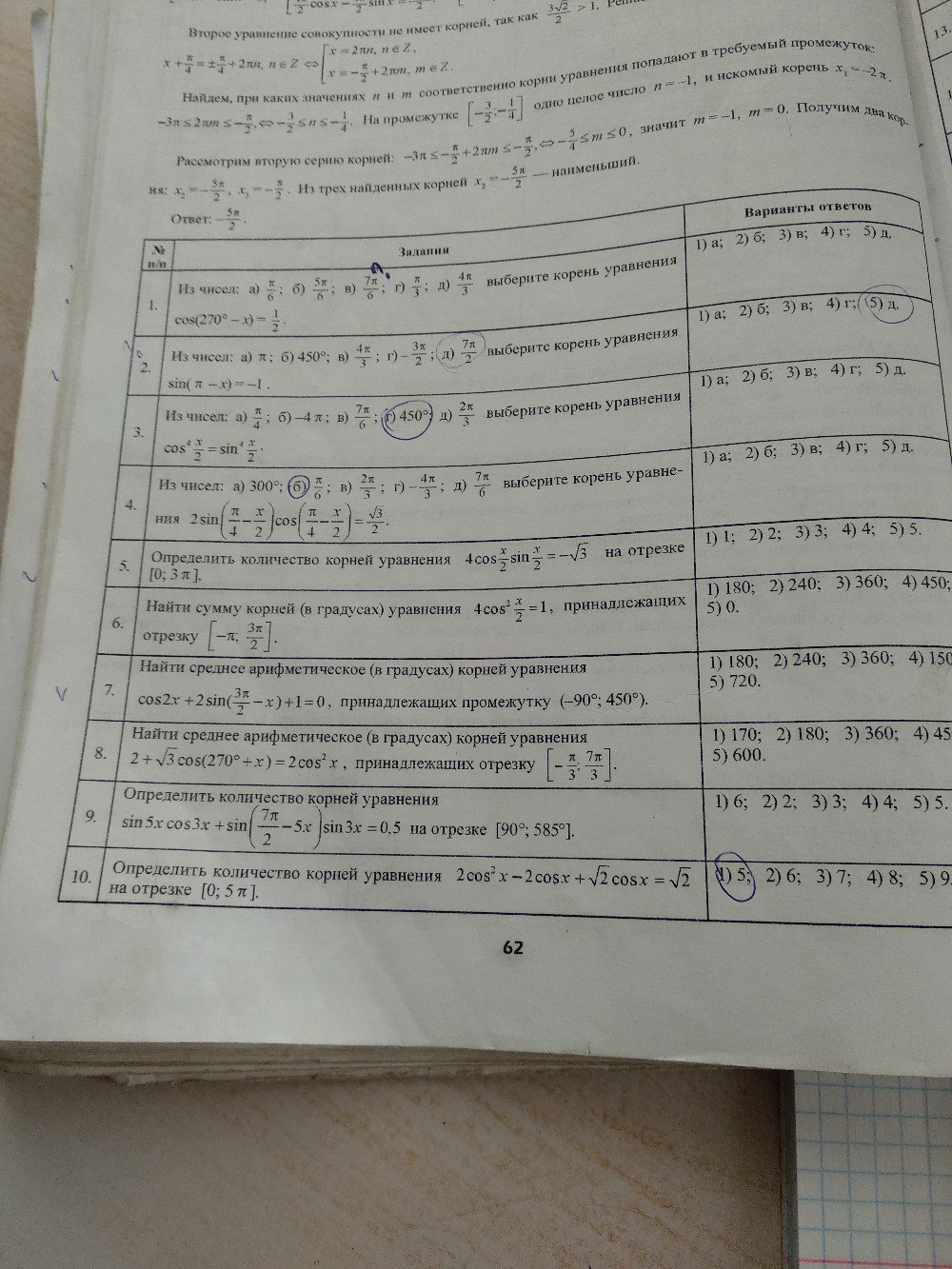
Ответы

Автор ответа: Аноним

$2cos^2x-cosx(2- \sqrt{2})- \sqrt{2}=0$
Замена:
$cosx=a \\ -1 \leq a \leq 1 \\ \\ 2a^2-(2- \sqrt{2})a- \sqrt{2}=0 \\ D=(2- \sqrt{2})^2+4*2* \sqrt{2}=6+4 \sqrt{2}=(2+ \sqrt{2})^2 \\ \\ a_1= \frac{2- \sqrt{2}-2- \sqrt{2} }{4} =- \frac{ \sqrt{2} }{2} \\ \\ a_2= \frac{2- \sqrt{2}+2+ \sqrt{2} }{4}=2$
$a_2$ не подходит
решаем:
$cosx=- \frac{ \sqrt{2} }{2} \\ \\ x=\pm ( \pi - \frac{ \pi }{4})+2 \pi k, k \in Z \\ \\ x=\pm \frac{3 \pi }{4}+2 \pi k, k \in Z \\ \\ 0 \leq x \leq 900$

$\left \{ {{x= \frac{3 \pi }{4}+2 \pi k, k \in Z } \atop {x=2 \pi k- \frac{3 \pi }{4}, k \in Z }} \right.$
подставляем в первое ур-е:
$k=0 ; \ x= \frac{3 \pi }{4} \\ \\ k=1; \ x= \frac{11 \pi }{4} \\ \\ k=2; \ x= \frac{19 \pi }{4}$

подставляем во второе ур-е:
$k=0; \ x=- \frac{3 \pi }{4} \\ \\ k=1; \ x= \frac{5 \pi }{4} \\ \\ k=2; \ x= \frac{13 \pi }{4}$

Общее кол-во корней 6
Ответ: 6

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Русский язык, автор: sabinacvetkova443

морфологический рабор слова идущие

6 лет назад

Предмет: Физика, автор: abcd12344w46578

С польным решением и объяснием пожалуйста:

6 лет назад

Предмет: Русский язык, автор: opl1op

В каких сочетаниях возможна замена краткой формой прилагательных,в каких-нет?Объясните почему.

1)Больной вопрос-больной ребёнок.

2)Белый сахар-белый стих.

3)Чёрная тень-чёрная дыра.

4)Глухой согласный-глухой человек.

5)Тёплый квас-тёплый взгляд.

6)Чёрный свитер-чёрный день.

7)Круглый шар-круглая сирота.

8)Холодный ветер-холодный цвет.

9)Скорая помощь-скорое решение.

6 лет назад

Предмет: Математика, автор: моо2

купили 2 десятка пуговиц.пришили 20 пуговиц. Сколько пуговиц осталось

9 лет назад

Предмет: Математика, автор: Антон111222333

Сколько потребуется 5-литровых банок воды чтобы до самого верха (краткая запись)

9 лет назад