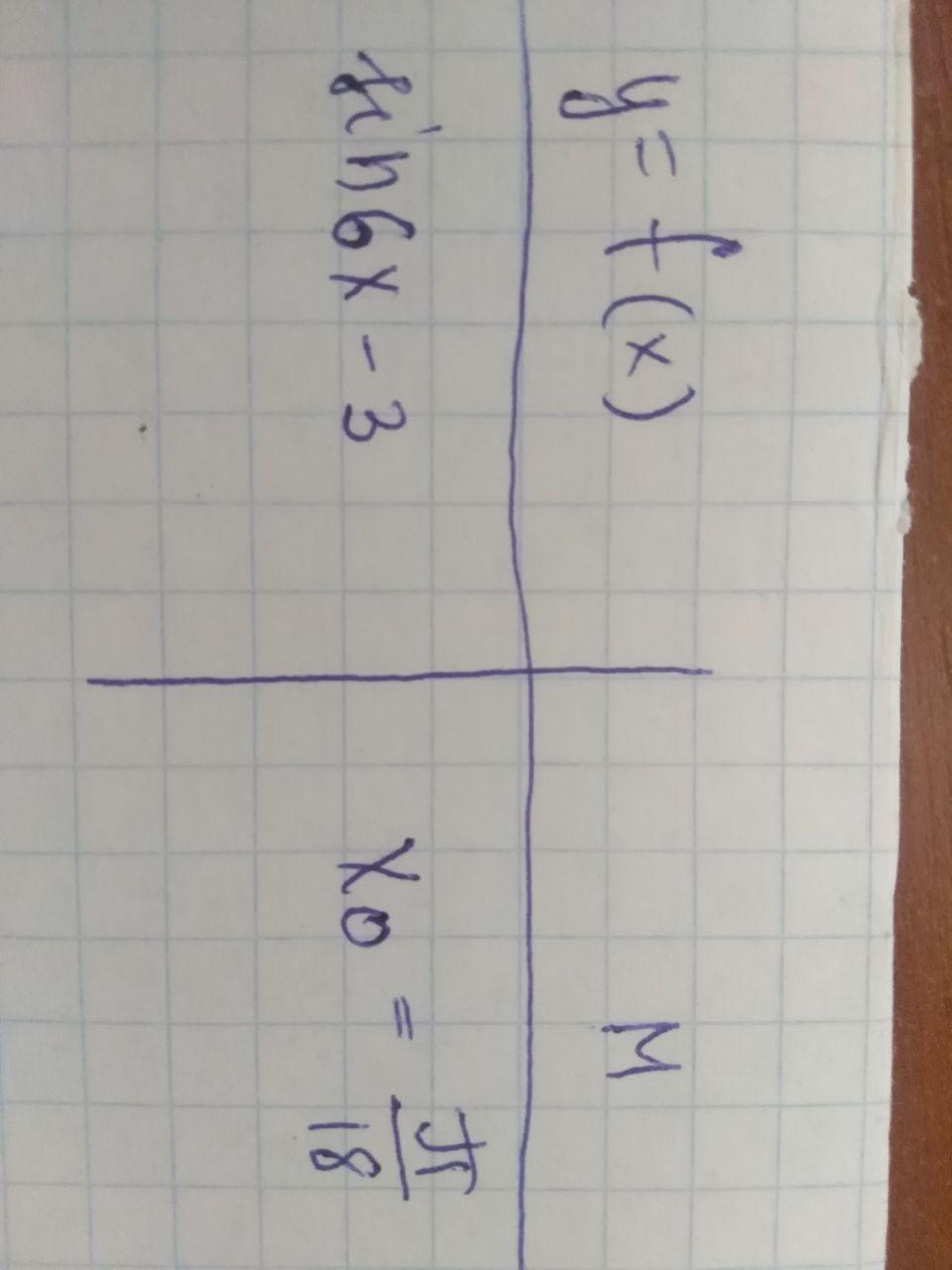
Записать уравнение касательной и нормаль к кривой y=f(x) в точке M(x(0),y(0)). Помогите плз)

касательная в х0
g(x)=f(x0)+f`(x0)(x-x0)
f(pi/18)=sin(6*pi/18)-3=sin(pi/3)-3=√3/2-3
f`(x)=6cos6x
f`(pi/18)=6*cos(6*pi/18)=6*cos(pi/3)=6*0.5=3
уравнение касательной g(x)=√3/2-3+3(x-pi/18)=√3/2-3+3x-pi/6=
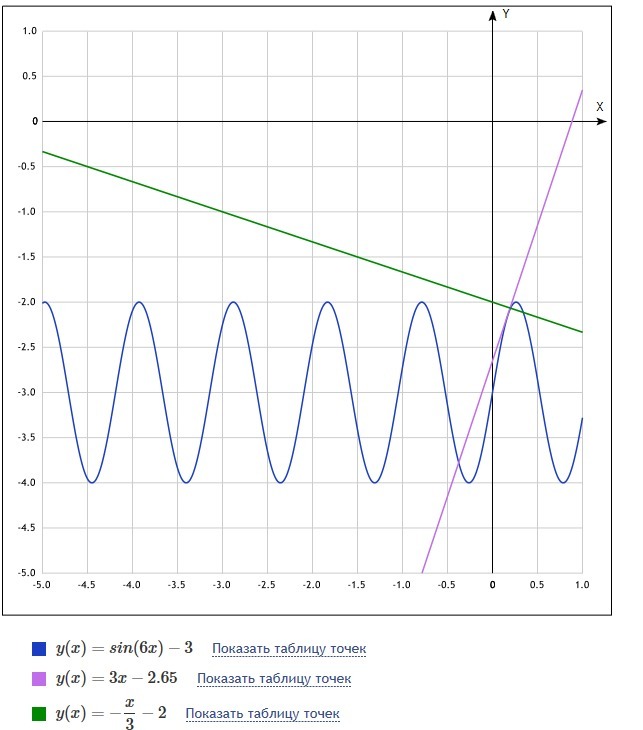
=3x-3+√3/2-3.14/6=3x-3+√3/2-0.52=3x-2.65
уравнение нормали в х0 y=f(x0)-(x-x0)/f`(x0)=√3/2-3-(x-pi/18)/3=-x/3-2