Предмет: Алгебра, автор: Topmc

sin7x-sin3x-cos5x=0
Помогите плиз

Ответы

Автор ответа: WhatYouNeed

6

$\displaystyle \sin{7x} -\sin{3x} -\cos{5x} =0$

Применим формулу разности синусов.

$\displaystyle 2\cos{\frac{7x+3x}2 } \sin{\frac{7x-3x}2 } -\cos {5x} =0$

Упростим дроби и разложим на множители.

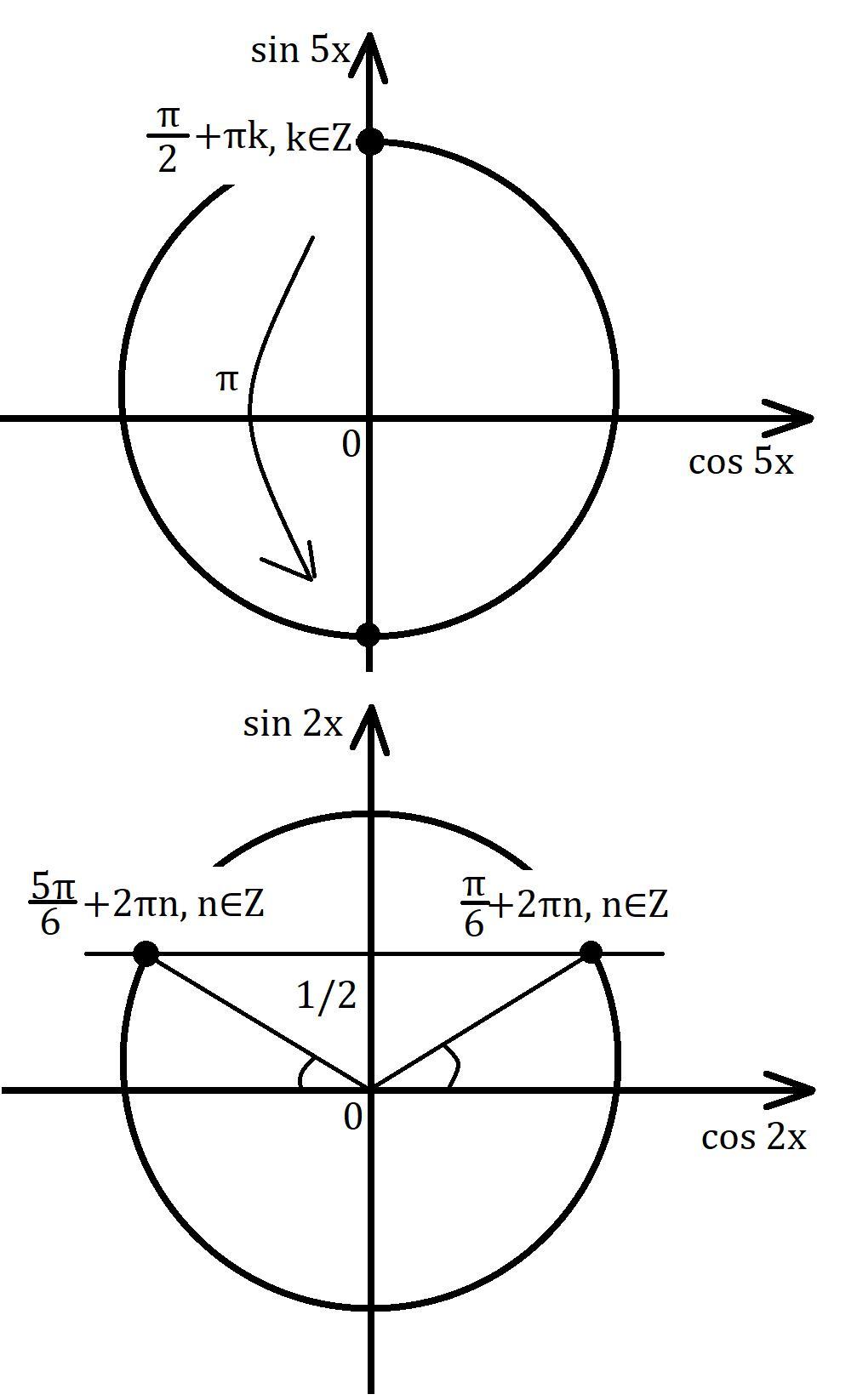
$\displaystyle 2\cos{5x} \sin{2x} -\cos{5x} =0\\\\ \cos{5x} \bigg( \sin{2x} -\frac12 \bigg) =0\\ \\ \begin{bmatrix} \displaystyle \cos{5x} =0\\ \displaystyle \sin{2x} =\frac12 \end{matirx}$

Решим простейшие тригонометрические уравнения и найдём x.

$\begin{bmatrix} \displaystyle 5x=\frac{\pi }2 +\pi k\qquad \\\\ \displaystyle 2x=\frac{\pi}6 +2\pi n\quad \\\\ \displaystyle 2x=\pi -\frac{\pi }6 +2\pi n\end{matirx} k,\! n\in \mathbb{Z}$

$\begin{bmatrix} \displaystyle x=\frac{\pi }{10} +\frac{\pi k}5\\\\ \displaystyle x=\frac{\pi}{12} +\pi n\\\\ \displaystyle x=\frac{5\pi }{12} +\pi n\end{matirx} k,\! n\in \mathbb{Z}$

Ответ: $\displaystyle x=\bigg \{ \frac{\pi }{10} +\frac{\pi k}5 ;\frac{\pi}{12} +\pi n; \frac{5\pi }{12} +\pi n\bigg \} ,k,\! n\in \mathbb{Z} .$

Приложения:

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Английский язык, автор: MOIN228

ПОМОГИТЕ СРОЧНО !!!!
Устный рассказ про Elizabeth II НА АНГЛИСКОМ!!. Объем не меньше 12 предл

6 лет назад

Предмет: Химия, автор: Popainota22800551166

найдите массу оксида бария если число его молекул равно 7.9 умножить на 10 в 23 степени

6 лет назад

Предмет: Алгебра, автор: sultanbektepbergen

Даны уравнения: 1) 7x² - 4x +9=0 2) 3x² - 8x +4=0 а) Определите, сколько корней имеет каждое уравнение? б) Найдите корни, если они существуют.

6 лет назад

Предмет: Математика, автор: ht39

Помогите решить пример!
Упростите выражение:

9 лет назад

Предмет: Химия, автор: rinka1821

Какую массу соли нужно добавить к 50 г 20%-ного раствора, чтобы увеличить её концентрацию в два раза? Ответ укажите в граммах с точностью до целых.

9 лет назад