Предмет: Алгебра, автор: Аноним

ПОМОГИТЕ ПОЖАЛУЙСТА 6 ИНТЕГРАЛОВ 100 БАЛЛОВ!!!!!!!!!!!!!!!

Приложения:

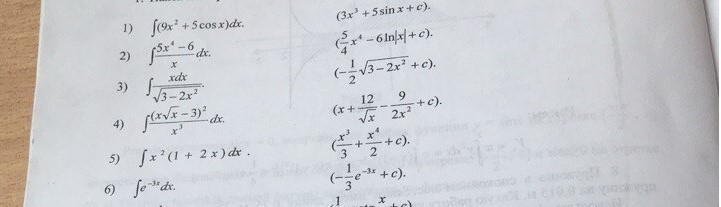
Ответы

Автор ответа: xtoto

(1)
$\int\limits {9x^2+5cos(x)} \, dx = 9*\int\limits {x^2} \, dx +5* \int\limits {cos(x)} \, dx =\\\\ =9*\frac{x^3}{3}+5*sin(x)+C=3x^3+5sin(x)+C$

(2)
$\int\limits {\frac{5x^4-6}{x}} \, dx = \int\limits {5x^3-\frac{6}{x}} \, dx =\\\\ =5* \int\limits {x^3} \, dx -6* \int\limits^a_b {\frac{1}{x}} \, dx =\\\\ =5*\frac{x^4}{4}-6*ln|x|+C=\\\\ =\frac{5}{4}x^4-6*ln|x|+C$

(3)
$\int\limits {\frac{x}{\sqrt{3-2x^2}}} \, dx = \int\limits {\frac{2x}{2\sqrt{3-2x^2}}} \, dx = \int\limits {\frac{1}{2\sqrt{3-2x^2}}} \, d(x^2) =\\\\= \int\limits {\frac{1}{-4\sqrt{3-2x^2}}} \, d(-2x^2)=\int\limits {\frac{1}{-4\sqrt{3-2x^2}}} \, d(3-2x^2)=\\\\ =[t=3-2x^2]=-\frac{1}{4}* \int\limits {\frac{1}{\sqrt{t}}} \, dt=-\frac{1}{4}* \int\limits {t^{-\frac{1}{2}}} \, dt=\\\\ =-\frac{1}{4}*\frac{t^{\frac{1}{2}}}{\frac{1}{2}}+C=-\frac{\sqrt{t}}{2}+C=-\frac{\sqrt{3-2x^2}}{2}+C$

(4)
$\int\limits {\frac{(x\sqrt{x}-3)^2}{x^3}} \, dx = \int\limits {\frac{x^3-6x^{\frac{3}{2}}-9}{x^3}} \, dx = \int\limits {1} \, dx -6 \int\limits^a_b {x^{-\frac{3}{2}}} \, dx - 9*\int\limits {x^{-3}} \, dx =\\\\ =x-6*\frac{x^{-\frac{1}{2}}}{-\frac{1}{2}}-9*\frac{x^{-2}}{-2}+C=\\\\ =x+\frac{12}{\sqrt{x}}+\frac{9}{2x^2}+C$

(5)
$\int\limits {x^2(1+2x)} \, dx = \int\limits {x^2+2x^3} \, dx = \int\limits {x^2} \, dx +2* \int\limits {x^3} \, dx =\\\\=\frac{x^3}{3}+2*\frac{x^4}{4}+C= \frac{x^3}{3}+\frac{x^4}{2}+C$

(6)
$\int\limits {e^{-3x}} \, dx = \int\limits {\frac{e^{-3x}}{-3}} \, d(-3x) =[t=-3x]=\\\\=-\frac{1}{3}* \int\limits {e^t} \, dt=-\frac{1}{3}e^t+C=\\\\ =-\frac{1}{3}e^{-3x}+C$

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Физика, автор: sosksbk

срочно даю 30 балов

В процессе работы тепловой машины за некоторое время рабочим телом было получено от нагревателя количество теплоты 1,8 МДж, передано холодильнику 1 МДж. Определи КПД тепловой машины

6 лет назад

Предмет: Математика, автор: duusshamooya

Упростите выражение:
1) - 5(4b + 3) - (b - 12) + 15(1+ 2b);
2) - 4(2,5d + 5) + 7(2 + 3d) - (d - 18);
3) 6(5a + 2) - (8 - a) - 2(10a - 4);
4) -3(8a - 4) + 2(12a +6) - 6(2 - 2a).

6 лет назад

Предмет: Обществознание, автор: aahahahahaa

мир моих увлечений (изо)
пожалуйста помогите сделайте его большим прошу...