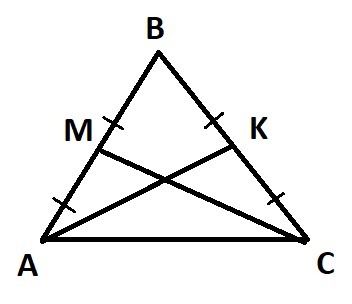
На боковых сторонах АВ и ВС равнобедренного треугольника АВС обозначили соответствующее точки М и К так, что ВМ=ВК. Докажите, что угол ВАК= углу ВСМ.

По условию, AB = BC (ΔABC равнобедренный),
MB = BK (по условию), ⇒ AM = KC.

Рассмотрим треугольники ΔABK и ΔBMC.
∠B - общий.
Так как MB = BK, AM = KC  и AB = AC,
то эти треугольники равны по двум сторонам и углу между ними.
--------------------------
Таким образом, углы ∠ВАК = ∠ВСМ.