В треугольнике АВС угол B вдвое больше угла С, а угол А - тупой. Точка К на стороне ВС такова, что угол КАС - прямой. Докажите, что КС=2АВ.

Объяснение:  Примем угол АСВ=х, тогда угол АВС=2х

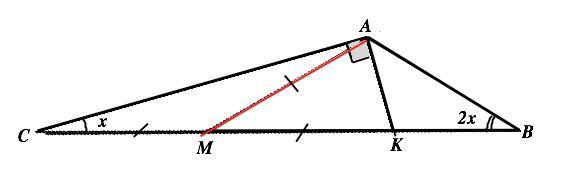
В прямоугольном ⊿ САК проведем медиану АМ. По свойству медианы прямоугольного треугольника АМ=СМ=КМ.

=> ∆ АМС равнобедренный, и угол МАС=угол АСМ=х.

  По свойству внешнего угла угол АМК при вершине М треугольника АМС равен сумме двух внутренних, не смежных с ним. => угол АМК=2х

В треугольнике МАВ углы при основании МВ равны 2х. Треугольник МАВ равнобедренный. АВ=АМ. Но КС=2 АМ, а т.к. АВ=АМ,  то КС=2АВ