Предмет: Алгебра, автор: HKarrison

Помогите пожалуйста с решением

Приложения:

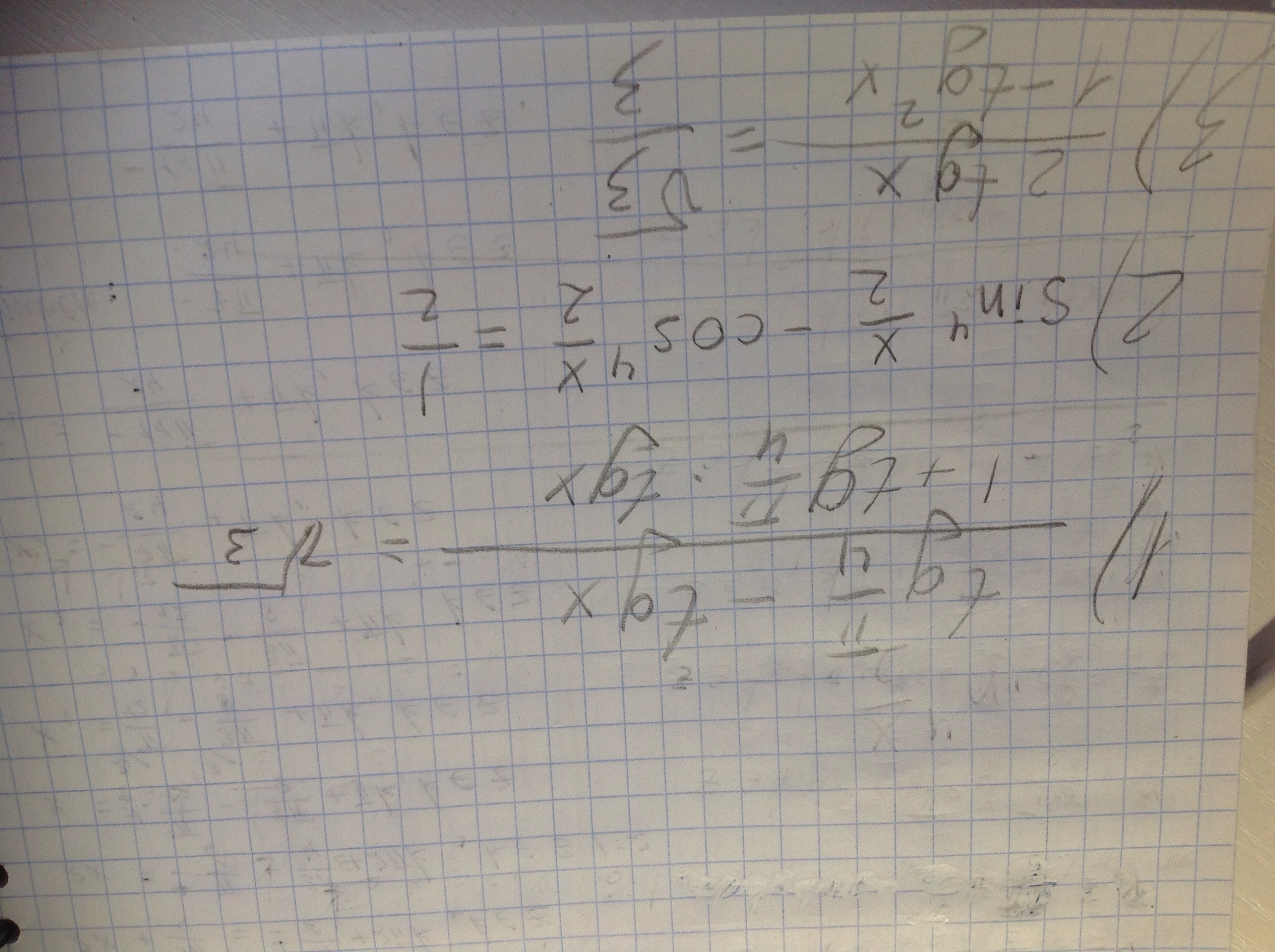
Ответы

Автор ответа: Аноним

1)
$tg( \frac{ \pi }{4}-x)= \sqrt{3} \\ \\ \frac{ \pi }{4}-x= \frac{ \pi }{3}+ \pi k , k \in Z \\ \\ -x= \frac{ \pi }{12}+ \pi k , k \in Z \ (*-1) \\ \\ x= - \frac{ \pi }{12}- \pi k , k \in Z$

2)
$sin^4 \frac{x}{4}-cos^4 \frac{x}{4} = \frac{1}{2} \\ \\ (sin^2 \frac{x}{4}-cos^2 \frac{x}{4} )(sin^2 \frac{x}{4}+cos^2 \frac{x}{4} )= \frac{1}{2} \\ \\ -(cos^2 \frac{x}{4} -sin^2 \frac{x}{4} )= \frac{1}{2} \\ \\ -cos \frac{x}{2} = \frac{1}{2} \\ \\ cos \frac{x}{2} =- \frac{1}{2} \\ \\ \frac{x}{2} =\pm \frac{2 \pi }{3}+2 \pi k , k \in Z \ (*2) \\ \\ x=\pm \frac{4 \pi }{3}+4 \pi k , k \in Z$

3)
$tg2x= \frac{ \sqrt{3} }{3} \\ \\ 2x= \frac{ \pi }{6}+ \pi k , k \in Z \ (:2) \\ \\ x= \frac{ \pi }{12}+ \frac{ \pi k}{2}, k \in Z$

* некоторые преобразования
1 пример
$tg(x-y)= \frac{tgx-tgy}{1+tgx*tgy}$
2 пример
$a^4-b^4=(a^2-b^2)(a^2+b^2)$
3 пример
$tg2x= \frac{2tgx}{1-tg^2x}$

Аноним: что не понятно пишите)

HKarrison: А как так складывается пример 1 и 3 до такого простого?

HKarrison: И во втором там же х/2 а не x/4

NNNLLL54: посмотрите формулы tg двойного угла...

HKarrison: Спасибо. Уже разобрался

Аноним: написал

Аноним: снизу