Предмет: Математика, автор: valeravasin

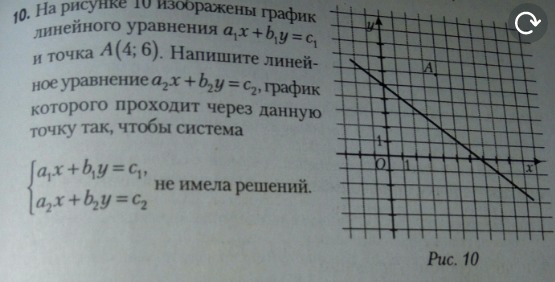
На рисунке изображён график линейного уравнения a1x+b1y=c1 и точка а(4,6). напишите линейное уравнение a2x+b2y=c2, график которого проходит через точку а, и система етих линейных уравнений не имела решения

Приложения:

Ответы

Автор ответа: WhatYouNeed

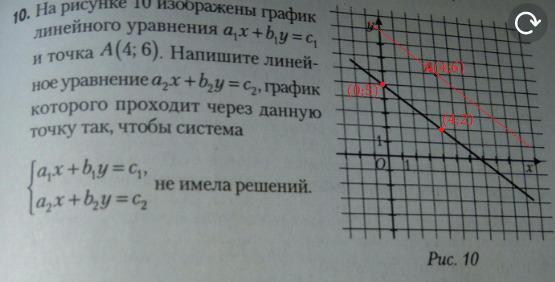
Прямая проходит через точки (0;5), (4;2). Подставим координаты точек в линейное уравнение a₁x+b₁y=c₁, составим систему и определим a₁, b₁ и с₁ с точностью до коэффициента.

$\displaystyle \left \{ {{a_1\cdot 0+b_1\cdot 5=c_1} \atop {a_1\cdot 4+b_1\cdot 2=c_1}} \right. \quad \left \{ {{c_1=5b_1\qquad \quad} \atop {4a_1+2b_1=5b_1}} \right. \\\\\left \{ {{c_1=5b_1} \atop {a_1=\dfrac34 b_1}} \right.$

Пусть b₁=4, тогда c₁=5·4=20, a₁=(3/4)·4=3

Получили уравнение 3x+4y=20

Система из условия не имеет решение, если графики линейных уравнений параллельны. Раз прямые параллельны, то коэффициенты при переменных равны с точностью до коэффициента.

Пусть a₂=3, тогда b₂=4

Координаты А(4;6) должны удовлетворять уравнению a₂x+b₂y=c₂

3·4+4·6=c₂=36

Получили уравнение 3x+4y=36

Ответ: 3x+4y=36.

Приложения: