Предмет: Алгебра,
автор: andreev20040109
Помогите решить уравнение пожалуйста!
Приложения:
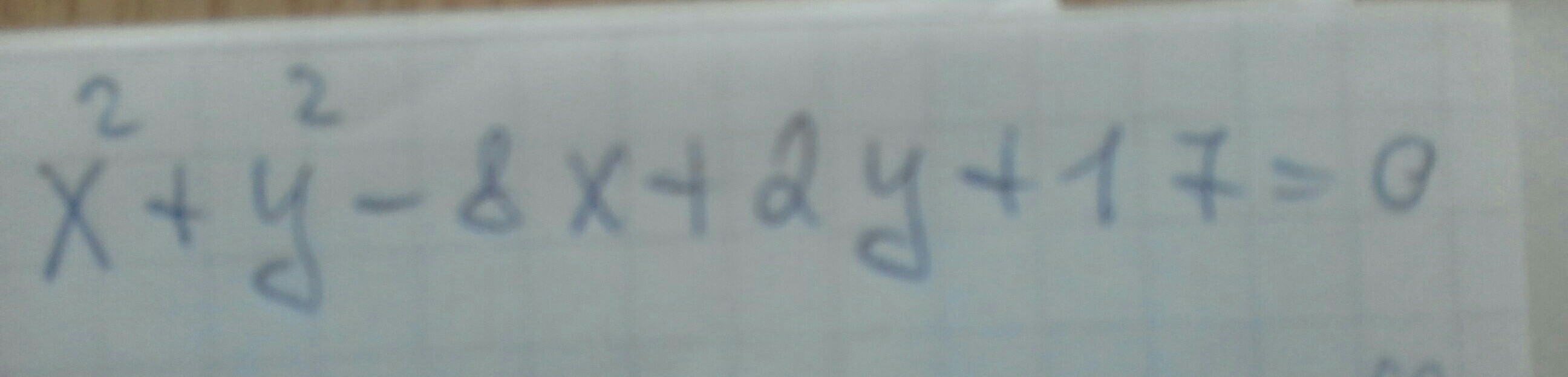
Ответы
Автор ответа:
1
x² + y² - 8x + 2y + 17 = 0
(x² - 8x + 16) + (y² + 2y + 1) = 0
(x - 4)² + (y + 1)² = 0
(x - 4)² ≥ 0 при любых значениях x
(y + 1)² ≥ 0 при любых значениях y
Значит сумма этих выражений равна нулю только в случае, когда
x - 4 = 0 ⇒ x = 4 и y + 1 = 0 ⇒ y = - 1
Ответ : x = 4 , y = - 1
(x² - 8x + 16) + (y² + 2y + 1) = 0
(x - 4)² + (y + 1)² = 0
(x - 4)² ≥ 0 при любых значениях x
(y + 1)² ≥ 0 при любых значениях y
Значит сумма этих выражений равна нулю только в случае, когда
x - 4 = 0 ⇒ x = 4 и y + 1 = 0 ⇒ y = - 1
Ответ : x = 4 , y = - 1
Интересные вопросы
Предмет: Английский язык,
автор: leylailaxa
Предмет: Английский язык,
автор: leylailaxa
Предмет: Биология,
автор: eugeniodepez
Предмет: Математика,
автор: Moonlight99
Предмет: Обществознание,
автор: YuliyaMedvedeva2015