В шаре на расстоянии 4 от центра проведено сечение, площадь которого 9п. Найти радиус шара

Ответ:

Радиус шара равен 5 единиц измерения

Объяснение:

В шаре на расстоянии 4 от центра проведено сечение, площадь которого 9п. Найти радиус шара.

• Сечение шара любой плоскостью (т.е. на любом расстоянии от центра шара и под любым углом) всегда будет кругом.

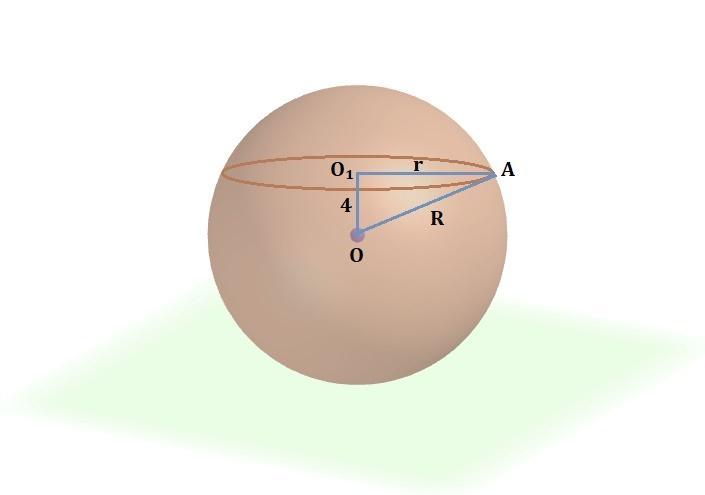
Имеем шар с центром в точке O и радиусом R=AO, который нам надо найти.

Сечение, пересекающее шар, пересекает ее по кругу, площадь которого 9π.

Поскольку площадь круга (радиусом r):

S = πr²,

то имеем:

9π=πr²  ⇒  3²=r²  ⇒ r=3 ед - радиус круга (нашего сечения).

Расстояние от центра шара до сечения – перпендикуляр опущенный из центра шара (точки О) до центра круга (точки О₁).

Из построения имеем: шар с радиусом R=AO, круг с радиусом r=AO₁=3 и OO₁=4  – расстояние от центра шара до сечения (OO₁⊥AO₁).

Из прямоугольного треугольника AO₁O (∠AO₁0=90°), по теореме Пифагора найдем гипотенузу AO=R – радиус шара:

AO²=OO₁²+AO₁² = 4²+3²=16+9=25

R=AO=√25=5 ед

#SPJ5