Предмет: Алгебра, автор: deadpool21

решить неравенство
2 log2(x корень из 5)- log2(x/1-x)меньше или равно log2(5x^2+1/x-2)

Приложения:

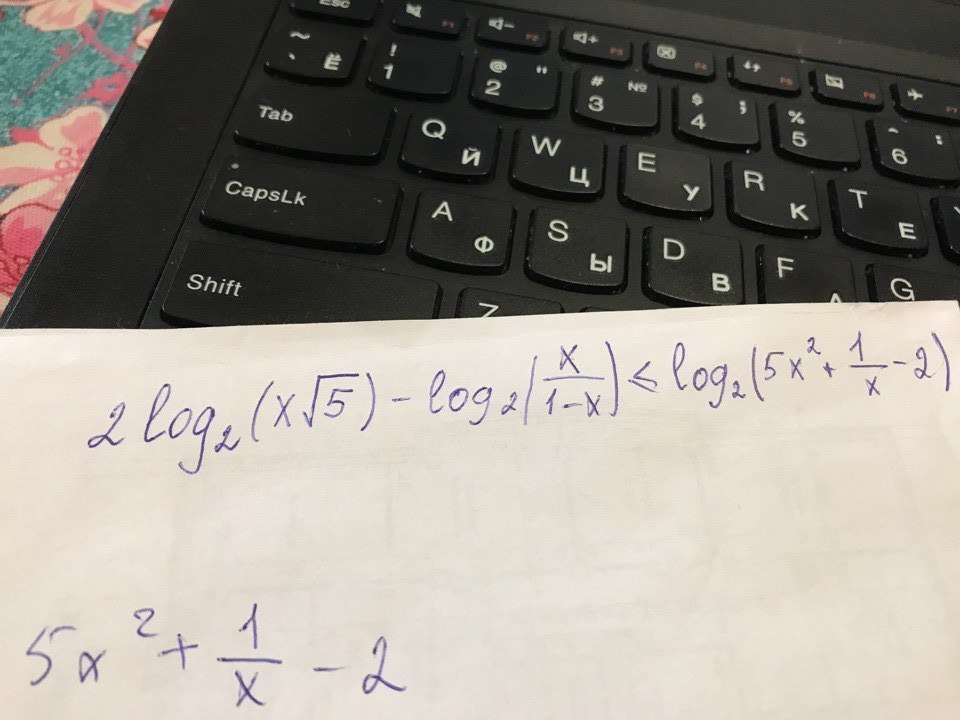
Ответы

Автор ответа: nelle987

Левая часть неравенства определена только при 0 < x < 1.
При таких x следующие переходы не меняют множество решений:
$\displaystyle 2\log_2(x\sqrt 5)-\log_2\left(\frac x{1-x}\right)\leqslant\log_2\left(5x^2+\frac1x-2\right)\\ \log_2\left(5x^2\cdot\frac{1-x}x\right)\leqslant\log_2\left(5x^2+\frac1x-2\right)\\ 5x(1-x)\leqslant5x^2+\frac1x-2\quad|\cdot x\ \textgreater \ 0\\ 5x^2(1-x)\leqslant5x^3-2x+1\\ 5x^2-5x^3\leqslant 5x^3-2x+1\\ 10x^3-5x^2-2x+1\geqslant0\\ 5x^2(2x-1)-(2x-1)\geqslant0\\ (5x^2-1)(2x-1)\geqslant0\\ \left(x+\frac{\sqrt5}5\right)\left(x-\frac{\sqrt5}5\right)\left(x-\frac12\right)\geqslant0$
В приведённых переходах имеет смысл пояснить только переход от второй строчки к третьей. Во-первых, логарифм по основанию 2 – возрастающая функция, так что знак при отбрасывании логарифмов остается прежним. Во-вторых, на 0 < x < 1 левая часть неравенства положительна, тогда правая часть (не меньшая левой) тоже положительна, значит, никаких дополнительных условий на положительность логарифмируемого выражения писать не нужно.

Полученное неравенство легко решается методом интервалов, получаем предварительный ответ
$\displaystyle x\in\left[-\frac{\sqrt5}5,\frac{\sqrt5}5\right]\cup\left[\frac12,\infty\right)$

После учета неравенства 0 < x < 1 окончательно имеем
$\displaystyle \boxed{x\in\left(0,\frac{\sqrt5}5\right]\cup\left[\frac12,1\right)}$

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Русский язык, автор: madinabonukhamrakulo

напишите пж сочинение на эту картину.

6 лет назад

Предмет: Обществознание, автор: onn197

коспект на тему труд-основа жизни

6 лет назад

Предмет: Математика, автор: acharlidomeulo

помогите пожалуйста
2:14=5:35
ПО ЭТАПНО СО ВСЕМИ ДЕЙСТВИЯМИ ПРОШУ!!

6 лет назад