Предмет: Алгебра, автор: Ap4i1337

СРОЧНО,завтра уже нужно здать. Скоротіть дріб a-9/√3+3

Ответы

Автор ответа: Аноним

У тебе в умовi помилка. Дивись додаток.

Приложения:

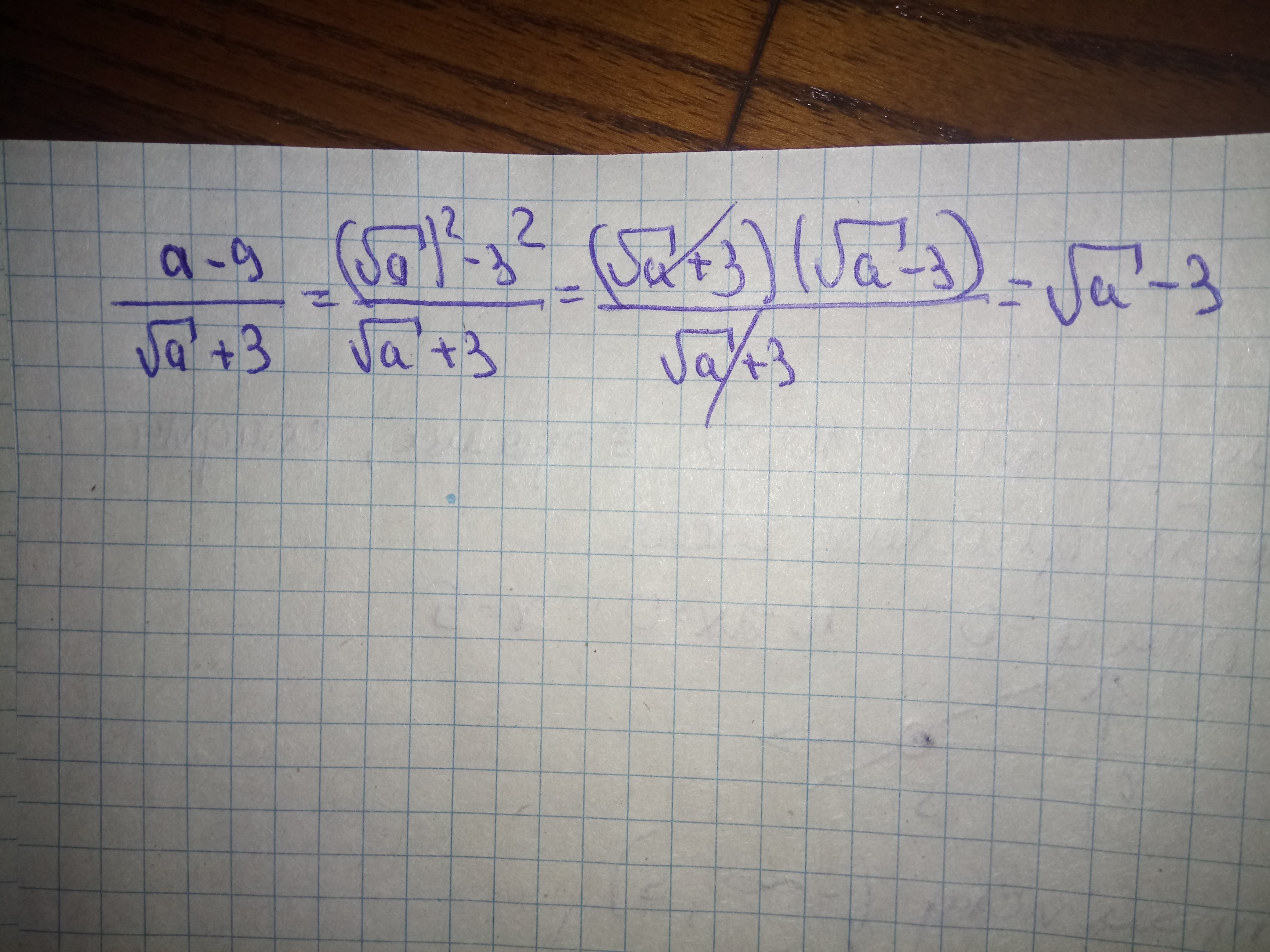
Автор ответа: tumanov2004

$a- \frac{9}{ \sqrt{3} } +3=a- \frac{9 \sqrt{3} }{ \sqrt{3} ^{2} } +3=a- \frac{9 \sqrt{3} }{3} +3= \frac{3a-9 \sqrt{3}+9 }{3}$

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Алгебра, автор: FandashHomie

Даю 30 баллов. Решить с помощью квадратного уравнения!!!

6 лет назад

Предмет: Русский язык, автор: diktorsolo

Составьте и запишите план текста из трёх пунктов.

Текст 2
(1)Однажды пригородный поезд не доехал до Москвы 15 километров и остановился. (2)«Долго будем "загорать"?» — поинтересовались два рослых пассажира. (3)«Как исправят, так и поедем», — ответил машинист. (4)«Нам ждать некогда, мы лучше на своих двоих», — сказали пассажиры и побежали. (5)Машинист засмеялся: «Какие шустрые, от поезда не убежите, догоню». (6)Но... не догнал. (7)Парни без труда пробежали оставшиеся 15 километров и за несколько минут до гудка поспели на завод.

(8)Это были знаменитые в 30-х годах двадцатого века стайеры — бегуны на длинные дистанции — братья Знаменские. (9)Серафим и Георгий работали на заводе «Серп и молот». (10)Оба красивые, статные, закалённые (круглый год ходили в лёгкой одежде, купались в реке), оба страстно любили спорт, соревнования считали праздником. (11)Каждую свободную минуту они тренировались, что не помешало им, рабочим парням, после обучения в мединституте стать врачами. (12)Оба не пользовались трамваем или автобусом: лучше лишний раз пробежаться! (13)За два года братья побили все рекорды в беге.

(14)«В чём секрет успеха бегуна?» — спросили однажды Серафима. (15)«Чтобы хорошо бегать, надо много бегать, бегать всюду: на соревнованиях и на тренировках, по асфальту и по рыхлому снегу, в лесу, в городе, быстро и медленно, в гору и с горы, утром и вечером», — ответил он. (16)Главное — бегать! (17)Только самозабвенная преданность спорту позволяет спортсменам достичь мировых рекордов, прославить свою страну. (18)И сегодня международные соревнования по лёгкой атлетике называются «Турнир братьев Знаменских». (19)В Москве их именем названы стадион и Олимпийский центр, а в Оренбурге — улица.

6 лет назад

Предмет: Физика, автор: kamillauser2007

181. Дві металеві кульки підвішені на штативах окремо одна від одної. Заряд однієї кульки дорівнює 5 нКл, а іншої - (-5 нКл). Кульки з'єднали. Який заряд кульок?

6 лет назад

Предмет: Математика, автор: Аноним

вычисли столбиком 75-55,1000-500,600-78

9 лет назад

Предмет: Право, автор: dmitrieva1232

Позначте усталені правила поведінки, що склались у суспільстві
в результаті їх тривалого повторення.
А норми права.
Б традиції та звичаї.
В норми моралі.
Г корпоративні норми.

9 лет назад